Formula for a tangent to the graph of a function. Equation of a tangent to the graph of a function. The Comprehensive Guide (2019)

A tangent is a straight line , which touches the graph of the function at one point and all points of which are at the shortest distance from the graph of the function. Therefore, the tangent passes tangent to the graph of the function at a certain angle, and several tangents at different angles cannot pass through the point of tangency. Tangent equations and normal equations to the graph of a function are constructed using the derivative.

The tangent equation is derived from the line equation .

Let us derive the equation of the tangent, and then the equation of the normal to the graph of the function.

y = kx + b .

In him k- angular coefficient.

From here we get the following entry:

y - y 0 = k(x - x 0 ) .

Derivative value f "(x 0 ) functions y = f(x) at the point x0 equal to the slope k= tg φ tangent to the graph of a function drawn through a point M0 (x 0 , y 0 ) , Where y0 = f(x 0 ) . This is geometric meaning of derivative .

Thus, we can replace k on f "(x 0 ) and get the following equation of the tangent to the graph of a function :

y - y 0 = f "(x 0 )(x - x 0 ) .

In problems involving composing the equation of a tangent to the graph of a function (and we will move on to them soon), it is required to reduce the equation obtained from the above formula to equation of a straight line in general form. To do this, you need to move all the letters and numbers to the left side of the equation, and leave zero on the right side.

Now about the normal equation. Normal - this is a straight line passing through the point of tangency to the graph of the function perpendicular to the tangent. Normal equation :

(x - x 0 ) + f "(x 0 )(y - y 0 ) = 0

To warm up, you are asked to solve the first example yourself, and then look at the solution. There is every reason to hope that this task will not be a “cold shower” for our readers.

Example 0. Create a tangent equation and a normal equation for the graph of a function at a point M (1, 1) .

Example 1. Write a tangent equation and a normal equation to the graph of a function , if the abscissa is tangent .

Let's find the derivative of the function:

Now we have everything that needs to be substituted into the entry given in the theoretical help to get the tangent equation. We get

In this example, we were lucky: the slope coefficient turned out to be zero, so there was no need to separately bring the equation to its general form. Now we can create the normal equation:

In the figure below: the graph of the function is burgundy, the tangent is green, the normal is orange.

The next example is also not complicated: the function, as in the previous one, is also a polynomial, but the slope will not be equal to zero, so one more step will be added - bringing the equation to a general form.

Example 2.

Solution. Let's find the ordinate of the tangent point:

Let's find the derivative of the function:

.

Let's find the value of the derivative at the point of tangency, that is, the slope of the tangent:

We substitute all the obtained data into the “blank formula” and get the tangent equation:

We bring the equation to its general form (we collect all letters and numbers other than zero on the left side, and leave zero on the right):

We compose the normal equation:

Example 3. Write the equation of the tangent and the equation of the normal to the graph of the function if the abscissa is the point of tangency.

Solution. Let's find the ordinate of the tangent point:

Let's find the derivative of the function:

.

Let's find the value of the derivative at the point of tangency, that is, the slope of the tangent:

.

We find the tangent equation:

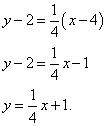
Before bringing the equation to its general form, you need to “comb it” a little: multiply term by term by 4. We do this and bring the equation to its general form:

We compose the normal equation:

Example 4. Write the equation of the tangent and the equation of the normal to the graph of the function if the abscissa is the point of tangency.

Solution. Let's find the ordinate of the tangent point:

.

Let's find the derivative of the function:

Let's find the value of the derivative at the point of tangency, that is, the slope of the tangent:

.

We get the tangent equation:

We bring the equation to its general form:

We compose the normal equation:

A common mistake when writing tangent and normal equations is not to notice that the function given in the example is complex and to calculate its derivative as the derivative of a simple function. The following examples are already from complex functions(the corresponding lesson will open in a new window).

Example 5. Write the equation of the tangent and the equation of the normal to the graph of the function if the abscissa is the point of tangency.

Solution. Let's find the ordinate of the tangent point:

Attention! This function is complex, since the tangent argument (2 x) is itself a function. Therefore, we find the derivative of a function as the derivative of a complex function.

The article provides a detailed explanation of the definitions, the geometric meaning of the derivative with graphic notations. The equation of a tangent line will be considered with examples, the equations of a tangent to 2nd order curves will be found.

Yandex.RTB R-A-339285-1 Definition 1

The angle of inclination of the straight line y = k x + b is called angle α, which is measured from the positive direction of the x axis to the straight line y = k x + b in the positive direction.

In the figure, the x direction is indicated by a green arrow and a green arc, and the angle of inclination by a red arc. The blue line refers to the straight line.

Definition 2

The slope of the straight line y = k x + b is called the numerical coefficient k.

The angular coefficient is equal to the tangent of the straight line, in other words k = t g α.

• The angle of inclination of a straight line is equal to 0 only if it is parallel about x and the slope is equal to zero, because the tangent of zero is equal to 0. This means the form of the equation will be y = b.
• If the angle of inclination of the straight line y = k x + b is acute, then the conditions 0 are satisfied< α < π 2 или 0 ° < α < 90 ° . Отсюда имеем, что значение углового коэффициента k считается положительным числом, потому как значение тангенс удовлетворяет условию t g α >0, and there is an increase in the graph.
• If α = π 2, then the location of the line is perpendicular to x. Equality is specified by x = c with the value c being a real number.
• If the angle of inclination of the straight line y = k x + b is obtuse, then it corresponds to the conditions π 2< α < π или 90 ° < α < 180 ° , значение углового коэффициента k принимает отрицательное значение, а график убывает.

A secant is a line that passes through 2 points of the function f (x). In other words, a secant is a straight line that passes through any two points on the graph of a given function.

The figure shows that A B is a secant, and f (x) is a black curve, α is a red arc, indicating the angle of inclination of the secant.

When the angular coefficient of a straight line is equal to the tangent of the angle of inclination, it is clear that the tangent of a right triangle A B C can be found by the ratio of the opposite side to the adjacent one.

Definition 4

We get a formula for finding a secant of the form:

k = t g α = B C A C = f (x B) - f x A x B - x A, where the abscissas of points A and B are the values ​​x A, x B, and f (x A), f (x B) are the values functions at these points.

Obviously, the angular coefficient of the secant is determined using the equality k = f (x B) - f (x A) x B - x A or k = f (x A) - f (x B) x A - x B, and the equation must be written as y = f (x B) - f (x A) x B - x A x - x A + f (x A) or
y = f (x A) - f (x B) x A - x B x - x B + f (x B) .

The secant divides the graph visually into 3 parts: to the left of point A, from A to B, to the right of B. The figure below shows that there are three secants that are considered coincident, that is, they are set using a similar equation.

By definition, it is clear that the straight line and its secant in this case coincide.

A secant can intersect the graph of a given function multiple times. If there is an equation of the form y = 0 for a secant, then the number of points of intersection with the sinusoid is infinite.

Definition 5

Tangent to the graph of the function f (x) at point x 0 ; f (x 0) is a straight line passing through a given point x 0; f (x 0), with the presence of a segment that has many x values ​​close to x 0.

Example 1

Let's take a closer look at the example below. Then it is clear that the line defined by the function y = x + 1 is considered tangent to y = 2 x at the point with coordinates (1; 2). For clarity, it is necessary to consider graphs with values ​​close to (1; 2). The function y = 2 x is shown in black, the blue line is the tangent line, and the red dot is the intersection point.

Obviously, y = 2 x merges with the line y = x + 1.

To determine the tangent, we should consider the behavior of the tangent A B as point B approaches point A infinitely. For clarity, we present a drawing.

The secant A B, indicated by the blue line, tends to the position of the tangent itself, and the angle of inclination of the secant α will begin to tend to the angle of inclination of the tangent itself α x.

Definition 6

The tangent to the graph of the function y = f (x) at point A is considered to be the limiting position of the secant A B as B tends to A, that is, B → A.

Now let's move on to consider the geometric meaning of the derivative of a function at a point.

Let's move on to considering the secant A B for the function f (x), where A and B with coordinates x 0, f (x 0) and x 0 + ∆ x, f (x 0 + ∆ x), and ∆ x is denoted as the increment of the argument . Now the function will take the form ∆ y = ∆ f (x) = f (x 0 + ∆ x) - f (∆ x) . For clarity, let's give an example of a drawing.

Consider the resulting right triangle A B C. We use the definition of tangent to solve, that is, we obtain the relation ∆ y ∆ x = t g α . From the definition of a tangent it follows that lim ∆ x → 0 ∆ y ∆ x = t g α x . According to the rule of the derivative at a point, we have that the derivative f (x) at the point x 0 is called the limit of the ratio of the increment of the function to the increment of the argument, where ∆ x → 0, then we denote it as f (x 0) = lim ∆ x → 0 ∆ y ∆ x .

It follows that f " (x 0) = lim ∆ x → 0 ∆ y ∆ x = t g α x = k x, where k x is denoted as the slope of the tangent.

That is, we find that f ' (x) can exist at point x 0, and like the tangent to a given graph of the function at the point of tangency equal to x 0, f 0 (x 0), where the value of the slope of the tangent at the point is equal to the derivative at point x 0 . Then we get that k x = f " (x 0) .

The geometric meaning of the derivative of a function at a point is that the concept of the existence of a tangent to the graph at the same point is given.

To write the equation of any straight line on a plane, it is necessary to have an angular coefficient with the point through which it passes. Its notation is taken to be x 0 at intersection.

The tangent equation to the graph of the function y = f (x) at the point x 0, f 0 (x 0) takes the form y = f "(x 0) x - x 0 + f (x 0).

This means that the final value of the derivative f "(x 0) can determine the position of the tangent, that is, vertically, provided lim x → x 0 + 0 f "(x) = ∞ and lim x → x 0 - 0 f "(x ) = ∞ or absence at all under the condition lim x → x 0 + 0 f " (x) ≠ lim x → x 0 - 0 f " (x) .

The location of the tangent depends on the value of its angular coefficient k x = f "(x 0). When parallel to the o x axis, we obtain that k k = 0, when parallel to o y - k x = ∞, and the form of the tangent equation x = x 0 increases with k x > 0, decreases as k x< 0 .

Example 2

Compile an equation for the tangent to the graph of the function y = e x + 1 + x 3 3 - 6 - 3 3 x - 17 - 3 3 at the point with coordinates (1; 3) and determine the angle of inclination.

Solution

By condition, we have that the function is defined for all real numbers. We find that the point with the coordinates specified by the condition, (1; 3) is a point of tangency, then x 0 = - 1, f (x 0) = - 3.

It is necessary to find the derivative at the point with value - 1. We get that

y " = e x + 1 + x 3 3 - 6 - 3 3 x - 17 - 3 3 " = = e x + 1 " + x 3 3 " - 6 - 3 3 x " - 17 - 3 3 " = e x + 1 + x 2 - 6 - 3 3 y " (x 0) = y " (- 1) = e - 1 + 1 + - 1 2 - 6 - 3 3 = 3 3

The value of f' (x) at the point of tangency is the slope of the tangent, which is equal to the tangent of the slope.

Then k x = t g α x = y " (x 0) = 3 3

It follows that α x = a r c t g 3 3 = π 6

Answer: the tangent equation takes the form

y = f " (x 0) x - x 0 + f (x 0) y = 3 3 (x + 1) - 3 y = 3 3 x - 9 - 3 3

For clarity, we give an example in a graphic illustration.

Black color is used for the graph of the original function, blue color is the image of the tangent, and the red dot is the point of tangency. The figure on the right shows an enlarged view.

Example 3

Determine the existence of a tangent to the graph of a given function
y = 3 · x - 1 5 + 1 at the point with coordinates (1 ; 1) . Write an equation and determine the angle of inclination.

Solution

By condition, we have that the domain of definition of a given function is considered to be the set of all real numbers.

Let's move on to finding the derivative

y " = 3 x - 1 5 + 1 " = 3 1 5 (x - 1) 1 5 - 1 = 3 5 1 (x - 1) 4 5

If x 0 = 1, then f' (x) is undefined, but the limits are written as lim x → 1 + 0 3 5 1 (x - 1) 4 5 = 3 5 1 (+ 0) 4 5 = 3 5 · 1 + 0 = + ∞ and lim x → 1 - 0 3 5 · 1 (x - 1) 4 5 = 3 5 · 1 (- 0) 4 5 = 3 5 · 1 + 0 = + ∞ , which means the existence vertical tangent at point (1; 1).

Answer: the equation will take the form x = 1, where the angle of inclination will be equal to π 2.

For clarity, let's depict it graphically.

Example 4

Find the points on the graph of the function y = 1 15 x + 2 3 - 4 5 x 2 - 16 5 x - 26 5 + 3 x + 2, where

1. There is no tangent;
2. The tangent is parallel to x;
3. The tangent is parallel to the line y = 8 5 x + 4.

Solution

It is necessary to pay attention to the scope of definition. By condition, we have that the function is defined on the set of all real numbers. We expand the module and solve the system with intervals x ∈ - ∞ ; 2 and [ - 2 ; + ∞) . We get that

y = - 1 15 x 3 + 18 x 2 + 105 x + 176 , x ∈ - ∞ ; - 2 1 15 x 3 - 6 x 2 + 9 x + 12 , x ∈ [ - 2 ; + ∞)

It is necessary to differentiate the function. We have that

y " = - 1 15 x 3 + 18 x 2 + 105 x + 176 " , x ∈ - ∞ ; - 2 1 15 x 3 - 6 x 2 + 9 x + 12 ", x ∈ [ - 2 ; + ∞) ⇔ y " = - 1 5 (x 2 + 12 x + 35) , x ∈ - ∞ ; - 2 1 5 x 2 - 4 x + 3 , x ∈ [ - 2 ; + ∞)

When x = − 2, then the derivative does not exist because the one-sided limits are not equal at that point:

lim x → - 2 - 0 y " (x) = lim x → - 2 - 0 - 1 5 (x 2 + 12 x + 35 = - 1 5 (- 2) 2 + 12 (- 2) + 35 = - 3 lim x → - 2 + 0 y " (x) = lim x → - 2 + 0 1 5 (x 2 - 4 x + 3) = 1 5 - 2 2 - 4 - 2 + 3 = 3

We calculate the value of the function at the point x = - 2, where we get that

1. y (- 2) = 1 15 - 2 + 2 3 - 4 5 (- 2) 2 - 16 5 (- 2) - 26 5 + 3 - 2 + 2 = - 2, that is, the tangent at the point (- 2; - 2) will not exist.
2. The tangent is parallel to x when the slope is zero. Then k x = t g α x = f "(x 0). That is, it is necessary to find the values ​​of such x when the derivative of the function turns it to zero. That is, the values ​​of f ' (x) will be the points of tangency, where the tangent is parallel to x .

When x ∈ - ∞ ; - 2, then - 1 5 (x 2 + 12 x + 35) = 0, and for x ∈ (- 2; + ∞) we get 1 5 (x 2 - 4 x + 3) = 0.

1 5 (x 2 + 12 x + 35) = 0 D = 12 2 - 4 35 = 144 - 140 = 4 x 1 = - 12 + 4 2 = - 5 ∈ - ∞ ; - 2 x 2 = - 12 - 4 2 = - 7 ∈ - ∞ ; - 2 1 5 (x 2 - 4 x + 3) = 0 D = 4 2 - 4 · 3 = 4 x 3 = 4 - 4 2 = 1 ∈ - 2 ; + ∞ x 4 = 4 + 4 2 = 3 ∈ - 2 ; +∞

Calculate the corresponding function values

y 1 = y - 5 = 1 15 - 5 + 2 3 - 4 5 - 5 2 - 16 5 - 5 - 26 5 + 3 - 5 + 2 = 8 5 y 2 = y (- 7) = 1 15 - 7 + 2 3 - 4 5 (- 7) 2 - 16 5 - 7 - 26 5 + 3 - 7 + 2 = 4 3 y 3 = y (1) = 1 15 1 + 2 3 - 4 5 1 2 - 16 5 1 - 26 5 + 3 1 + 2 = 8 5 y 4 = y (3) = 1 15 3 + 2 3 - 4 5 3 2 - 16 5 3 - 26 5 + 3 3 + 2 = 4 3

Hence - 5; 8 5, - 4; 4 3, 1; 8 5, 3; 4 3 are considered to be the required points of the function graph.

Let's look at a graphical representation of the solution.

The black line is the graph of the function, the red dots are the tangency points.

1. When the lines are parallel, the angular coefficients are equal. Then it is necessary to search for points on the function graph where the slope will be equal to the value 8 5. To do this, you need to solve an equation of the form y "(x) = 8 5. Then, if x ∈ - ∞; - 2, we obtain that - 1 5 (x 2 + 12 x + 35) = 8 5, and if x ∈ ( - 2 ; + ∞), then 1 5 (x 2 - 4 x + 3) = 8 5.

The first equation has no roots since the discriminant is less than zero. Let's write down that

1 5 x 2 + 12 x + 35 = 8 5 x 2 + 12 x + 43 = 0 D = 12 2 - 4 43 = - 28< 0

Another equation has two real roots, then

1 5 (x 2 - 4 x + 3) = 8 5 x 2 - 4 x - 5 = 0 D = 4 2 - 4 · (- 5) = 36 x 1 = 4 - 36 2 = - 1 ∈ - 2 ; + ∞ x 2 = 4 + 36 2 = 5 ∈ - 2 ; +∞

Let's move on to finding the values ​​of the function. We get that

y 1 = y (- 1) = 1 15 - 1 + 2 3 - 4 5 (- 1) 2 - 16 5 (- 1) - 26 5 + 3 - 1 + 2 = 4 15 y 2 = y (5) = 1 15 5 + 2 3 - 4 5 5 2 - 16 5 5 - 26 5 + 3 5 + 2 = 8 3

Points with values ​​- 1; 4 15, 5; 8 3 are the points at which the tangents are parallel to the line y = 8 5 x + 4.

Answer: black line – graph of the function, red line – graph of y = 8 5 x + 4, blue line – tangents at points - 1; 4 15, 5; 8 3.

There may be an infinite number of tangents for given functions.

Example 5

Write the equations of all available tangents of the function y = 3 cos 3 2 x - π 4 - 1 3, which are located perpendicular to the straight line y = - 2 x + 1 2.

Solution

To compile the tangent equation, it is necessary to find the coefficient and coordinates of the tangent point, based on the condition of perpendicularity of the lines. The definition is as follows: the product of angular coefficients that are perpendicular to straight lines is equal to - 1, that is, written as k x · k ⊥ = - 1. From the condition we have that the angular coefficient is located perpendicular to the line and is equal to k ⊥ = - 2, then k x = - 1 k ⊥ = - 1 - 2 = 1 2.

Now you need to find the coordinates of the touch points. You need to find x and then its value for a given function. Note that from the geometric meaning of the derivative at the point
x 0 we obtain that k x = y "(x 0). From this equality we find the values ​​of x for the points of tangency.

We get that

y " (x 0) = 3 cos 3 2 x 0 - π 4 - 1 3 " = 3 - sin 3 2 x 0 - π 4 3 2 x 0 - π 4 " = = - 3 sin 3 2 x 0 - π 4 3 2 = - 9 2 sin 3 2 x 0 - π 4 ⇒ k x = y " (x 0) ⇔ - 9 2 sin 3 2 x 0 - π 4 = 1 2 ⇒ sin 3 2 x 0 - π 4 = - 1 9

This trigonometric equation will be used to calculate the ordinates of the tangent points.

3 2 x 0 - π 4 = a r c sin - 1 9 + 2 πk or 3 2 x 0 - π 4 = π - a r c sin - 1 9 + 2 πk

3 2 x 0 - π 4 = - a r c sin 1 9 + 2 πk or 3 2 x 0 - π 4 = π + a r c sin 1 9 + 2 πk

x 0 = 2 3 π 4 - a r c sin 1 9 + 2 πk or x 0 = 2 3 5 π 4 + a r c sin 1 9 + 2 πk , k ∈ Z

Z is a set of integers.

x points of contact have been found. Now you need to move on to searching for the values ​​of y:

y 0 = 3 cos 3 2 x 0 - π 4 - 1 3

y 0 = 3 1 - sin 2 3 2 x 0 - π 4 - 1 3 or y 0 = 3 - 1 - sin 2 3 2 x 0 - π 4 - 1 3

y 0 = 3 1 - - 1 9 2 - 1 3 or y 0 = 3 - 1 - - 1 9 2 - 1 3

y 0 = 4 5 - 1 3 or y 0 = - 4 5 + 1 3

From this we obtain that 2 3 π 4 - a r c sin 1 9 + 2 πk ; 4 5 - 1 3 , 2 3 5 π 4 + a r c sin 1 9 + 2 πk ; - 4 5 + 1 3 are the points of tangency.

Answer: the necessary equations will be written as

y = 1 2 x - 2 3 π 4 - a r c sin 1 9 + 2 πk + 4 5 - 1 3 , y = 1 2 x - 2 3 5 π 4 + a r c sin 1 9 + 2 πk - 4 5 + 1 3 , k ∈ Z

For a visual representation, consider a function and a tangent on a coordinate line.

The figure shows that the function is located on the interval [ - 10 ; 10 ], where the black line is the graph of the function, the blue lines are tangents, which are located perpendicular to the given line of the form y = - 2 x + 1 2. Red dots are touch points.

The canonical equations of 2nd order curves are not single-valued functions. Tangent equations for them are compiled according to known schemes.

Tangent to a circle

To define a circle with center at point x c e n t e r ; y c e n t e r and radius R, apply the formula x - x c e n t e r 2 + y - y c e n t e r 2 = R 2 .

This equality can be written as a union of two functions:

y = R 2 - x - x c e n t e r 2 + y c e n t e r y = - R 2 - x - x c e n t e r 2 + y c e n t e r

The first function is located at the top, and the second at the bottom, as shown in the figure.

To compose the equation of a circle at the point x 0; y 0 , which is located in the upper or lower semicircle, you should find the equation of the graph of a function of the form y = R 2 - x - x c e n t e r 2 + y c e n t e r or y = - R 2 - x - x c e n t e r 2 + y c e n t e r at the indicated point.

When at points x c e n t e r ; y c e n t e r + R and x c e n t e r ; y c e n t e r - R tangents can be given by the equations y = y c e n t e r + R and y = y c e n t e r - R , and at points x c e n t e r + R ; y c e n t e r and
x c e n t e r - R ; y c e n t e r will be parallel to o y, then we obtain equations of the form x = x c e n t e r + R and x = x c e n t e r - R .

Tangent to an ellipse

When the ellipse has a center at x c e n t e r ; y c e n t e r with semi-axes a and b, then it can be specified using the equation x - x c e n t e r 2 a 2 + y - y c e n t e r 2 b 2 = 1.

An ellipse and a circle can be denoted by combining two functions, namely the upper and lower half-ellipse. Then we get that

y = b a · a 2 - (x - x c e n t e r) 2 + y c e n t e r y = - b a · a 2 - (x - x c e n t e r) 2 + y c e n t e r

If the tangents are located at the vertices of the ellipse, then they are parallel about x or about y. Below, for clarity, consider the figure.

Example 6

Write the equation of the tangent to the ellipse x - 3 2 4 + y - 5 2 25 = 1 at points with values ​​of x equal to x = 2.

Solution

It is necessary to find the tangent points that correspond to the value x = 2. We substitute into the existing equation of the ellipse and find that

x - 3 2 4 x = 2 + y - 5 2 25 = 1 1 4 + y - 5 2 25 = 1 ⇒ y - 5 2 = 3 4 25 ⇒ y = ± 5 3 2 + 5

Then 2 ; 5 3 2 + 5 and 2; - 5 3 2 + 5 are the tangent points that belong to the upper and lower half-ellipse.

Let's move on to finding and solving the equation of the ellipse with respect to y. We get that

x - 3 2 4 + y - 5 2 25 = 1 y - 5 2 25 = 1 - x - 3 2 4 (y - 5) 2 = 25 1 - x - 3 2 4 y - 5 = ± 5 1 - x - 3 2 4 y = 5 ± 5 2 4 - x - 3 2

Obviously, the upper half-ellipse is specified using a function of the form y = 5 + 5 2 4 - x - 3 2, and the lower half ellipse y = 5 - 5 2 4 - x - 3 2.

Let's apply a standard algorithm to create an equation for a tangent to the graph of a function at a point. Let us write that the equation for the first tangent at point 2; 5 3 2 + 5 will look like

y " = 5 + 5 2 4 - x - 3 2 " = 5 2 1 2 4 - (x - 3) 2 4 - (x - 3) 2 " = = - 5 2 x - 3 4 - ( x - 3) 2 ⇒ y " (x 0) = y " (2) = - 5 2 2 - 3 4 - (2 - 3) 2 = 5 2 3 ⇒ y = y " (x 0) x - x 0 + y 0 ⇔ y = 5 2 3 (x - 2) + 5 3 2 + 5

We find that the equation of the second tangent with a value at the point
2 ; - 5 3 2 + 5 takes the form

y " = 5 - 5 2 4 - (x - 3) 2 " = - 5 2 1 2 4 - (x - 3) 2 4 - (x - 3) 2 " = = 5 2 x - 3 4 - (x - 3) 2 ⇒ y " (x 0) = y " (2) = 5 2 2 - 3 4 - (2 - 3) 2 = - 5 2 3 ⇒ y = y " (x 0) x - x 0 + y 0 ⇔ y = - 5 2 3 (x - 2) - 5 3 2 + 5

Graphically, tangents are designated as follows:

Tangent to hyperbole

When a hyperbola has a center at x c e n t e r ; y c e n t e r and vertices x c e n t e r + α ; y c e n t e r and x c e n t e r - α ; y c e n t e r , the inequality x - x c e n t e r 2 α 2 - y - y c e n t e r 2 b 2 = 1 takes place, if with vertices x c e n t e r ; y c e n t e r + b and x c e n t e r ; y c e n t e r - b , then is specified using the inequality x - x c e n t e r 2 α 2 - y - y c e n t e r 2 b 2 = - 1 .

A hyperbola can be represented as two combined functions of the form

y = b a · (x - x c e n t e r) 2 - a 2 + y c e n t e r y = - b a · (x - x c e n t e r) 2 - a 2 + y c e n t e r or y = b a · (x - x c e n t e r) 2 + a 2 + y c e n t e r y = - b a · (x - x c e n t e r) 2 + a 2 + y c e n t e r

In the first case we have that the tangents are parallel to y, and in the second they are parallel to x.

It follows that in order to find the equation of the tangent to a hyperbola, it is necessary to find out which function the point of tangency belongs to. To determine this, it is necessary to substitute into the equations and check for identity.

Example 7

Write an equation for the tangent to the hyperbola x - 3 2 4 - y + 3 2 9 = 1 at point 7; - 3 3 - 3 .

Solution

It is necessary to transform the solution record for finding a hyperbola using 2 functions. We get that

x - 3 2 4 - y + 3 2 9 = 1 ⇒ y + 3 2 9 = x - 3 2 4 - 1 ⇒ y + 3 2 = 9 x - 3 2 4 - 1 ⇒ y + 3 = 3 2 x - 3 2 - 4 and y + 3 = - 3 2 x - 3 2 - 4 ⇒ y = 3 2 x - 3 2 - 4 - 3 y = - 3 2 x - 3 2 - 4 - 3

It is necessary to identify which function a given point with coordinates 7 belongs to; - 3 3 - 3 .

Obviously, to check the first function it is necessary y (7) = 3 2 · (7 - 3) 2 - 4 - 3 = 3 3 - 3 ≠ - 3 3 - 3, then the point does not belong to the graph, since the equality does not hold.

For the second function we have that y (7) = - 3 2 · (7 - 3) 2 - 4 - 3 = - 3 3 - 3 ≠ - 3 3 - 3, which means the point belongs to the given graph. From here you should find the slope.

We get that

y " = - 3 2 (x - 3) 2 - 4 - 3 " = - 3 2 x - 3 (x - 3) 2 - 4 ⇒ k x = y " (x 0) = - 3 2 x 0 - 3 x 0 - 3 2 - 4 x 0 = 7 = - 3 2 7 - 3 7 - 3 2 - 4 = - 3

Answer: the tangent equation can be represented as

y = - 3 x - 7 - 3 3 - 3 = - 3 x + 4 3 - 3

It is clearly depicted like this:

Tangent to a parabola

To create an equation for the tangent to the parabola y = a x 2 + b x + c at the point x 0, y (x 0), you must use a standard algorithm, then the equation will take the form y = y "(x 0) x - x 0 + y ( x 0). Such a tangent at the vertex is parallel to x.

You should define the parabola x = a y 2 + b y + c as the union of two functions. Therefore, we need to solve the equation for y. We get that

x = a y 2 + b y + c ⇔ a y 2 + b y + c - x = 0 D = b 2 - 4 a (c - x) y = - b + b 2 - 4 a (c - x) 2 a y = - b - b 2 - 4 a (c - x) 2 a

Let's depict it graphically as:

To find out whether a point x 0, y (x 0) belongs to a function, proceed gently according to the standard algorithm. Such a tangent will be parallel to o y relative to the parabola.

Example 8

Write the equation of the tangent to the graph x - 2 y 2 - 5 y + 3 when we have a tangent angle of 150 °.

Solution

We begin the solution by representing the parabola as two functions. We get that

2 y 2 - 5 y + 3 - x = 0 D = (- 5) 2 - 4 · (- 2) · (3 - x) = 49 - 8 x y = 5 + 49 - 8 x - 4 y = 5 - 49 - 8 x - 4

The value of the slope is equal to the value of the derivative at point x 0 of this function and is equal to the tangent of the angle of inclination.

We get:

k x = y " (x 0) = t g α x = t g 150 ° = - 1 3

From here we determine the x value for the points of contact.

The first function will be written as

y " = 5 + 49 - 8 x - 4 " = 1 49 - 8 x ⇒ y " (x 0) = 1 49 - 8 x 0 = - 1 3 ⇔ 49 - 8 x 0 = - 3

Obviously, there are no real roots, since we got a negative value. We conclude that there is no tangent with an angle of 150° for such a function.

The second function will be written as

y " = 5 - 49 - 8 x - 4 " = - 1 49 - 8 x ⇒ y " (x 0) = - 1 49 - 8 x 0 = - 1 3 ⇔ 49 - 8 x 0 = - 3 x 0 = 23 4 ⇒ y (x 0) = 5 - 49 - 8 23 4 - 4 = - 5 + 3 4

We have that the points of contact are 23 4 ; - 5 + 3 4 .

Answer: the tangent equation takes the form

y = - 1 3 x - 23 4 + - 5 + 3 4

Let's depict it graphically this way:

If you notice an error in the text, please highlight it and press Ctrl+Enter

The video lesson “Equation of a tangent to the graph of a function” demonstrates educational material for mastering the topic. During the video lesson, the theoretical material necessary to formulate the concept of the equation of a tangent to the graph of a function at a given point, an algorithm for finding such a tangent, and examples of solving problems using the studied theoretical material are described.

The video tutorial uses methods that improve the clarity of the material. The presentation contains drawings, diagrams, important voice comments, animation, highlighting and other tools.

The video lesson begins with a presentation of the topic of the lesson and an image of a tangent to the graph of some function y=f(x) at the point M(a;f(a)). It is known that the angular coefficient of the tangent plotted to the graph at a given point is equal to the derivative of the function f΄(a) at this point. Also from the algebra course we know the equation of the straight line y=kx+m. The solution to the problem of finding the tangent equation at a point is schematically presented, which reduces to finding the coefficients k, m. Knowing the coordinates of a point belonging to the graph of the function, we can find m by substituting the coordinate value into the tangent equation f(a)=ka+m. From it we find m=f(a)-ka. Thus, knowing the value of the derivative at a given point and the coordinates of the point, we can represent the tangent equation in this way y=f(a)+f΄(a)(x-a).

The following is an example of composing a tangent equation following the diagram. Given the function y=x 2 , x=-2. Taking a=-2, we find the value of the function at a given point f(a)= f(-2)=(-2) 2 =4. We determine the derivative of the function f΄(x)=2x. At this point the derivative is equal to f΄(a)= f΄(-2)=2·(-2)=-4. To compose the equation, all coefficients a=-2, f(a)=4, f΄(a)=-4 were found, so the tangent equation is y=4+(-4)(x+2). Simplifying the equation, we get y = -4-4x.

The following example suggests constructing an equation for the tangent at the origin to the graph of the function y=tgx. At a given point a=0, f(0)=0, f΄(x)=1/cos 2 x, f΄(0)=1. So the tangent equation looks like y=x.

As a generalization, the process of composing an equation tangent to the graph of a function at a certain point is formalized in the form of an algorithm consisting of 4 steps:

• Enter the designation a for the abscissa of the tangent point;
• f(a) is calculated;
• f΄(x) is determined and f΄(a) is calculated. The found values ​​of a, f(a), f΄(a) are substituted into the tangent equation formula y=f(a)+f΄(a)(x-a).

Example 1 considers composing the tangent equation to the graph of the function y=1/x at point x=1. To solve the problem we use an algorithm. For a given function at point a=1, the value of the function f(a)=-1. Derivative of the function f΄(x)=1/x 2. At point a=1 the derivative f΄(a)= f΄(1)=1. Using the data obtained, the tangent equation y=-1+(x-1), or y=x-2, is drawn up.

In example 2, it is necessary to find the equation of the tangent to the graph of the function y=x 3 +3x 2 -2x-2. The main condition is the parallelism of the tangent and straight line y=-2x+1. First, we find the angular coefficient of the tangent, equal to the angular coefficient of the straight line y=-2x+1. Since f΄(a)=-2 for a given line, then k=-2 for the desired tangent. We find the derivative of the function (x 3 +3x 2 -2x-2)΄=3x 2 +6x-2. Knowing that f΄(a)=-2, we find the coordinates of point 3a 2 +6a-2=-2. Having solved the equation, we get a 1 =0, and 2 =-2. Using the found coordinates, you can find the tangent equation using a well-known algorithm. We find the value of the function at the points f(a 1)=-2, f(a 2)=-18. The value of the derivative at the point f΄(а 1)= f΄(а 2)=-2. Substituting the found values ​​into the tangent equation, we obtain for the first point a 1 =0 y=-2x-2, and for the second point a 2 =-2 the tangent equation y=-2x-22.

Example 3 describes the composition of the tangent equation for drawing it at the point (0;3) to the graph of the function y=√x. The solution is made using a well-known algorithm. The tangent point has coordinates x=a, where a>0. The value of the function at the point f(a)=√x. The derivative of the function f΄(х)=1/2√х, therefore at a given point f΄(а)=1/2√а. Substituting all the obtained values ​​into the tangent equation, we obtain y = √a + (x-a)/2√a. Transforming the equation, we get y=x/2√а+√а/2. Knowing that the tangent passes through the point (0;3), we find the value of a. We find a from 3=√a/2. Hence √a=6, a=36. We find the tangent equation y=x/12+3. The figure shows the graph of the function under consideration and the constructed desired tangent.

Students are reminded of the approximate equalities Δy=≈f΄(x)Δxand f(x+Δx)-f(x)≈f΄(x)Δx. Taking x=a, x+Δx=x, Δx=x-a, we get f(x)- f(a)≈f΄(a)(x-a), hence f(x)≈f(a)+ f΄(a)(x-a).

In example 4, it is necessary to find the approximate value of the expression 2.003 6. Since it is necessary to find the value of the function f(x)=x 6 at the point x=2.003, we can use the well-known formula, taking f(x)=x 6, a=2, f(a)= f(2)=64, f ΄(x)=6x 5. Derivative at the point f΄(2)=192. Therefore, 2.003 6 ≈65-192·0.003. Having calculated the expression, we get 2.003 6 ≈64.576.

The video lesson “Equation of a tangent to the graph of a function” is recommended for use in a traditional mathematics lesson at school. For a teacher teaching remotely, video material will help explain the topic more clearly. The video can be recommended for students to review independently if necessary to deepen their understanding of the subject.

TEXT DECODING:

We know that if a point M (a; f(a)) (em with coordinates a and ef from a) belongs to the graph of the function y = f (x) and if at this point it is possible to draw a tangent to the graph of the function that is not perpendicular to the axis abscissa, then the angular coefficient of the tangent is equal to f"(a) (eff prime from a).

Let a function y = f(x) and a point M (a; f(a)) be given, and it is also known that f´(a) exists. Let's create an equation for the tangent to the graph of a given function at a given point. This equation, like the equation of any straight line that is not parallel to the ordinate axis, has the form y = kx+m (the y is equal to ka x plus em), so the task is to find the values ​​of the coefficients k and m. (ka and em)

Angle coefficient k= f"(a). To calculate the value of m, we use the fact that the desired straight line passes through the point M(a; f (a)). This means that if we substitute the coordinates of the point M into the equation of the straight line, we obtain the correct equality : f(a) = ka+m, from where we find that m = f(a) - ka.

It remains to substitute the found values ​​of the coefficients ki and m into the equation of the straight line:

y = kx+(f(a) -ka);

y = f(a)+k(x-a);

y= f(a)+ f"(a) (x- a). ( y is equal to ef from a plus ef prime from a, multiplied by x minus a).

We have obtained the equation for the tangent to the graph of the function y = f(x) at the point x=a.

If, say, y = x 2 and x = -2 (i.e. a = -2), then f (a) = f (-2) = (-2) 2 = 4; f´(x) = 2x, which means f"(a) = f´(-2) = 2·(-2) = -4. (then the ef of a is equal to four, the ef of the prime of x is equal to two x, which means ef prime from a equals minus four)

Substituting the found values ​​a = -2, f(a) = 4, f"(a) = -4 into the equation, we obtain: y = 4+(-4)(x+2), i.e. y = -4x -4.

(E is equal to minus four x minus four)

Let's create an equation for the tangent to the graph of the function y = tanx (the y is equal to the tangent x) at the origin. We have: a = 0, f(0) = tan0=0;

f"(x)= , which means f"(0) = l. Substituting the found values ​​a=0, f(a)=0, f´(a) = 1 into the equation, we get: y=x.

Let us summarize our steps in finding the equation of the tangent to the graph of a function at point x using an algorithm.

ALGORITHM FOR DEVELOPING AN EQUATION FOR A TANGENT TO THE GRAPH OF THE FUNCTION y = f(x):

1) Designate the abscissa of the tangent point with the letter a.

2) Calculate f(a).

3) Find f´(x) and calculate f´(a).

4) Substitute the found numbers a, f(a), f´(a) into the formula y= f(a)+ f"(a) (x- a).

Example 1. Create an equation for the tangent to the graph of the function y = - in

point x = 1.

Solution. Let's use the algorithm, taking into account that in this example

2) f(a)=f(1)=- =-1

3) f´(x)=; f´(a)= f´(1)= =1.

4) Substitute the found three numbers: a = 1, f(a) = -1, f"(a) = 1 into the formula. We get: y = -1+(x-1), y = x-2.

Answer: y = x-2.

Example 2. Given a function y = x 3 +3x 2 -2x-2. Write down the equation of the tangent to the graph of the function y = f(x), parallel to the straight line y = -2x +1.

Using the algorithm for composing the tangent equation, we take into account that in this example f(x) = x 3 +3x 2 -2x-2, but the abscissa of the tangent point is not indicated here.

Let's start thinking like this. The desired tangent must be parallel to the straight line y = -2x+1. And parallel lines have equal angular coefficients. This means that the angular coefficient of the tangent is equal to the angular coefficient of the given straight line: k tangent. = -2. Hok cas. = f"(a). Thus, we can find the value of a from the equation f ´(a) = -2.

Let's find the derivative of the function y=f(x):

f"(x)= (x 3 +3x 2 -2x-2)´ =3x 2 +6x-2;f"(a)= 3a 2 +6a-2.

From the equation f"(a) = -2, i.e. 3a 2 +6a-2=-2 we find a 1 =0, a 2 =-2. This means that there are two tangents that satisfy the conditions of the problem: one at the point with abscissa 0, the other at the point with abscissa -2.

Now you can follow the algorithm.

1) a 1 =0, and 2 =-2.

2) f(a 1)= 0 3 +3·0 2 -2∙0-2=-2; f(a 2)= (-2) 3 +3·(-2) 2 -2·(-2)-2=6;

3) f"(a 1) = f"(a 2) = -2.

4) Substituting the values ​​a 1 = 0, f(a 1) = -2, f"(a 1) = -2 into the formula, we get:

y=-2-2(x-0), y=-2x-2.

Substituting the values ​​a 2 = -2, f(a 2) =6, f"(a 2) = -2 into the formula, we get:

y=6-2(x+2), y=-2x+2.

Answer: y=-2x-2, y=-2x+2.

Example 3. From point (0; 3) draw a tangent to the graph of the function y = . Solution. Let's use the algorithm for composing the tangent equation, taking into account that in this example f(x) = . Note that here, as in example 2, the abscissa of the tangent point is not explicitly indicated. Nevertheless, we follow the algorithm.

1) Let x = a be the abscissa of the point of tangency; it is clear that a >0.

3) f´(x)=()´=; f´(a) =.

4) Substituting the values ​​of a, f(a) = , f"(a) = into the formula

y=f (a) +f "(a) (x-a), we get:

By condition, the tangent passes through the point (0; 3). Substituting the values ​​x = 0, y = 3 into the equation, we get: 3 = , and then =6, a =36.

As you can see, in this example, only at the fourth step of the algorithm we managed to find the abscissa of the tangent point. Substituting the value a =36 into the equation, we get: y=+3

In Fig. Figure 1 shows a geometric illustration of the considered example: a graph of the function y = is plotted, a straight line is drawn y = +3.

Answer: y = +3.

We know that for a function y = f(x), which has a derivative at point x, the approximate equality is valid: Δyf´(x)Δx (delta y is approximately equal to the eff prime of x multiplied by delta x)

or, in more detail, f(x+Δx)-f(x) f´(x) Δx (eff from x plus delta x minus ef from x is approximately equal to eff prime from x by delta x).

For the convenience of further reasoning, let us change the notation:

instead of x we ​​will write A,

instead of x+Δx we will write x

Instead of Δx we will write x-a.

Then the approximate equality written above will take the form:

f(x)-f(a)f´(a)(x-a)

f(x)f(a)+f´(a)(x-a). (eff from x is approximately equal to ef from a plus ef prime from a, multiplied by the difference between x and a).

Example 4. Find the approximate value of the numerical expression 2.003 6.

Solution. We are talking about finding the value of the function y = x 6 at the point x = 2.003. Let's use the formula f(x)f(a)+f´(a)(x-a), taking into account that in this example f(x)=x 6, a = 2,f(a) = f(2) = 2 6 =64; x = 2.003, f"(x) = 6x 5 and, therefore, f"(a) = f"(2) = 6 2 5 =192.

As a result we get:

2.003 6 64+192· 0.003, i.e. 2.003 6 =64.576.

If we use a calculator, we get:

2,003 6 = 64,5781643...

As you can see, the approximation accuracy is quite acceptable.

Job type: 7

Condition

The straight line y=3x+2 is tangent to the graph of the function y=-12x^2+bx-10.

Show solution

Solution

Let x_0 be the abscissa of the point on the graph of the function y=-12x^2+bx-10 through which the tangent to this graph passes. The value of the derivative at point x_0 is equal to the slope of the tangent, that is, y"(x_0)=-24x_0+b=3. On the other hand, the point of tangency belongs simultaneously to both the graph of the function and the tangent, that is, -12x_0^2+bx_0-10= 3x_0+2. We get a system of equations

\begin(cases) -24x_0+b=3,\\-12x_0^2+bx_0-10=3x_0+2. \end(cases)

Solving this system, we get x_0^2=1, which means either x_0=-1 or x_0=1.

Job type: 7
According to the abscissa condition, the tangent points are less than zero, so x_0=-1, then b=3+24x_0=-21.

Condition

Answer

Show solution

Topic: Geometric meaning of derivatives. Tangent to the graph of a function

The straight line y=-3x+4 is parallel to the tangent to the graph of the function y=-x^2+5x-7.

Solving this system, we get x_0^2=1, which means either x_0=-1 or x_0=1.

Find the abscissa of the tangent point.

Job type: 7
According to the abscissa condition, the tangent points are less than zero, so x_0=-1, then b=3+24x_0=-21.

Condition

Show solution

The angular coefficient of the straight line to the graph of the function y=-x^2+5x-7 at an arbitrary point x_0 is equal to y"(x_0). But y"=-2x+5, which means y"(x_0)=-2x_0+5. Angular the coefficient of the line y=-3x+4 specified in the condition is equal to -3. Parallel lines have the same angular coefficients. Therefore, we find a value of x_0 such that =-2x_0 +5=-3.

As is known, tg(\pi -\alpha) will be the value of the derivative of the function f(x) at point x_0. notice, that tg \alpha =\frac(AC)(CB)=\frac(2-1)(-1-(-6))=\frac15. From here, using the reduction formulas, we get:

Solving this system, we get x_0^2=1, which means either x_0=-1 or x_0=1.

Find the abscissa of the tangent point.

Job type: 7
According to the abscissa condition, the tangent points are less than zero, so x_0=-1, then b=3+24x_0=-21.

Condition

tg(\pi -\alpha) =-tg \alpha =-\frac15=-0.2.

Show solution

The straight line y=-2x-4 is tangent to the graph of the function y=16x^2+bx+12.

Find b, given that the abscissa of the tangent point is greater than zero.

Let x_0 be the abscissa of the point on the graph of the function y=16x^2+bx+12 through which is tangent to this graph.

The value of the derivative at point x_0 is equal to the slope of the tangent, that is, y"(x_0)=32x_0+b=-2. On the other hand, the point of tangency belongs simultaneously to both the graph of the function and the tangent, that is, 16x_0^2+bx_0+12=- 2x_0-4. We obtain a system of equations

Solving this system, we get x_0^2=1, which means either x_0=-1 or x_0=1.

Find the abscissa of the tangent point.

Job type: 7
According to the abscissa condition, the tangent points are less than zero, so x_0=-1, then b=3+24x_0=-21.

Condition

\begin(cases) 32x_0+b=-2,\\16x_0^2+bx_0+12=-2x_0-4. \end(cases)

Show solution

Solving the system, we get x_0^2=1, which means either x_0=-1 or x_0=1.

Solving this system, we get x_0^2=1, which means either x_0=-1 or x_0=1.

Find the abscissa of the tangent point.

Job type: 7
According to the abscissa condition, the tangent points are less than zero, so x_0=-1, then b=3+24x_0=-21.

Condition

According to the abscissa condition, the tangent points are greater than zero, so x_0=1, then b=-2-32x_0=-34.

Show solution

The figure shows a graph of the function y=f(x), defined on the interval (-2; 8).

Solving this system, we get x_0^2=1, which means either x_0=-1 or x_0=1.

Find the abscissa of the tangent point.

Job type: 7
According to the abscissa condition, the tangent points are less than zero, so x_0=-1, then b=3+24x_0=-21.

Condition

Determine the number of points at which the tangent to the graph of the function is parallel to the straight line y=6.

Show solution

The straight line y=6 is parallel to the Ox axis. Therefore, we find points at which the tangent to the graph of the function is parallel to the Ox axis.

On this chart, such points are extremum points (maximum or minimum points). As you can see, there are 4 extremum points.

The straight line y=4x-6 is parallel to the tangent to the graph of the function y=x^2-4x+9.

If now point P is shifted along the graph to point M, then straight line MR will rotate around point M. In this case, ∆x will tend to zero. From here we can formulate the definition of a tangent to the graph of a function.

Tangent to the graph of a function

The tangent to the graph of a function is the limiting position of the secant as the increment of the argument tends to zero. It should be understood that the existence of the derivative of the function f at the point x0 means that at this point of the graph there is tangent to him.

In this case, the angular coefficient of the tangent will be equal to the derivative of this function at this point f’(x0). This is the geometric meaning of the derivative. The tangent to the graph of a function f differentiable at point x0 is a certain straight line passing through the point (x0;f(x0)) and having an angular coefficient f’(x0).

Tangent equation

Let's try to obtain the equation of the tangent to the graph of some function f at point A(x0; f(x0)). The equation of a straight line with slope k has the following form:

Since our slope coefficient is equal to the derivative f’(x0), then the equation will take the following form: y = f’(x0)*x + b.

Now let's calculate the value of b. To do this, we use the fact that the function passes through point A.

f(x0) = f’(x0)*x0 + b, from here we express b and get b = f(x0) - f’(x0)*x0.

We substitute the resulting value into the tangent equation:

y = f’(x0)*x + b = f’(x0)*x + f(x0) - f’(x0)*x0 = f(x0) + f’(x0)*(x - x0).

y = f(x0) + f’(x0)*(x - x0).

Consider the following example: find the equation of the tangent to the graph of the function f(x) = x 3 - 2*x 2 + 1 at point x = 2.

2. f(x0) = f(2) = 2 2 - 2*2 2 + 1 = 1.

3. f’(x) = 3*x 2 - 4*x.

4. f’(x0) = f’(2) = 3*2 2 - 4*2 = 4.

5. Substitute the obtained values ​​into the tangent formula, we get: y = 1 + 4*(x - 2). Opening the brackets and bringing similar terms we get: y = 4*x - 7.

Answer: y = 4*x - 7.

General scheme for composing the tangent equation to the graph of the function y = f(x):

1. Determine x0.

2. Calculate f(x0).

3. Calculate f’(x)