Řešení rovnice 5. stupně. Rovnice vyšších stupňů. Rovnice vyšších stupňů s celočíselnými koeficienty

V 16. století narazili matematici na komplexní čísla téměř náhodou (viz kapitola 11). V 18. století byla komplexní čísla považována za rozšíření oboru reálných čísel, ale práce s nimi stále vedla k chybám parity, protože skvělá práce Leonarda E. o teorii čísel, Aritmetická vyšetřování (1801), se vyhýbala použití tzv. „imaginární čísla“. Zdá se mi, že nejdůležitější částí této práce je první důkaz základní věty algebry. Gauss si uvědomil, jak důležitá je tato věta, a během následujících let přinesl několik dalších důkazů. V roce 1849 přepracoval první verzi, tentokrát s použitím komplexních čísel. V moderních termínech můžeme říci, že pro jakoukoli konečnou polynomickou rovnici s reálnými nebo komplexními koeficienty budou všechny její kořeny reálnými nebo komplexními čísly. Dostáváme tak negativní odpověď na dlouhodobou otázku, zda řešení polynomických rovnic vyšších řádů vyžaduje generování čísel vyššího řádu, než jsou komplexní.

Jedním z nejožehavějších problémů algebry té doby byla otázka, zda lze polynom pátého řádu, kvintiku, vyřešit algebraickými metodami, tedy pomocí konečného počtu algebraických kroků. Dnes se ve škole učí vzorec pro řešení kvadratických rovnic a od 16. století jsou známy podobné metody pro řešení rovnic třetího a čtvrtého stupně (kapitola 11). Ale nebyla nalezena jediná metoda pro kvintiku. Může se zdát, že základní věta algebry má vyhlídku na kladnou odpověď, ale ve skutečnosti pouze zaručuje, že řešení existují, neříká nic o existenci vzorců, které dávají přesná řešení (přibližné numerické a grafické metody již tehdy existovaly ). A pak se objevili dva matematickí géniové s tragickým osudem.

Niels Henrik Abel (1802–1829) se narodil do velké chudé rodiny žijící v malé vesnici v Norsku, zemi zdevastované dlouhými roky války s Anglií a Švédskem. Učitel, který byl k chlapci laskavý, mu dával soukromé hodiny, ale po smrti svého otce, ve věku osmnácti let, byl Abel navzdory svému nízkému věku a křehkému zdraví nucen živit rodinu. V roce 1824 publikoval vědecký článek, ve kterém uvedl, že kvintika není řešitelná algebraickými prostředky, stejně jako jakýkoli polynom vyššího řádu. Abel věřil, že tento článek poslouží jako jeho vstupenka do vědeckého světa, a poslal jej Gaussovi na univerzitu v Göttingenu. Gauss se bohužel nikdy nedostal k řezání stránek nožem (to v té době musel dělat každý čtenář) a článek nečetl. V roce 1826 norská vláda konečně poskytla Abelovi finanční prostředky na cestování po Evropě. Ze strachu, že mu osobní komunikace s Gaussem nepřinese mnoho radosti, se matematik rozhodl nenavštívit Göttingen a místo toho odjel do Berlína. Tam se spřátelil s Augustem Leopoldem Krellem (1780–1855), matematikem, architektem a inženýrem, který radil pruskému ministerstvu školství v otázkách matematiky. Krell zamýšlel založit Journal of Pure and Applied Mathematics. Abel tak dostal příležitost své dílo šířit a hodně publikoval, zejména v prvních číslech Journalu, který okamžitě začal být považován za velmi prestižní a autoritativní vědeckou publikaci. Nor tam zveřejnil rozšířenou verzi svého důkazu, že kvintika je nerozhodnutelná algebraickými metodami. A pak odjel do Paříže. Tento výlet Abela velmi rozrušil, protože od francouzských matematiků prakticky nedostal potřebnou podporu. Sblížil se s Augustinem Louisem Cauchym (1789–1857), který byl v té době předním představitelem matematické analýzy, ale měl velmi komplexní charakter. Jak řekl sám Ábel: "Cauchy je šílený a nedá se s tím nic dělat, ačkoli v současnosti je jediný, kdo je v matematice něčeho schopen." Pokusíme-li se ospravedlnit projevy neúcty a zanedbávání vycházející z Gausse a Cauchyho, můžeme říci, že kvintik dosáhl určité slávy a přitáhl pozornost jak uznávaných matematiků, tak originalistů. Abel se vrátil do Norska, kde stále více trpěl tuberkulózou. Pokračoval v odesílání své práce do Crelle, ale zemřel v roce 1829, aniž by si byl vědom toho, jak moc se jeho pověst ve vědeckém světě prosadila. Dva dny po jeho smrti dostal Abel nabídku zaujmout vědecké místo v Berlíně.

Abel ukázal, že jakýkoli polynom nad čtvrtým řádem nelze vyřešit pomocí radikálů, jako jsou odmocniny, krychlové odmocniny nebo ty vyššího řádu. Explicitní podmínky, za kterých lze ve speciálních případech tyto polynomy řešit, a způsob jejich řešení však formuloval Galois. Évariste Galois (1811–1832) žil krátký a rušný život. Byl to neuvěřitelně nadaný matematik. Galois byl nemilosrdný k těm, které považoval za méně talentované než on sám, a zároveň nenáviděl sociální nespravedlnost. Neukázal žádné nadání pro matematiku, dokud si nepřečetl Legendrovy Prvky geometrie (vydané v roce 1794, tato kniha byla hlavní učebnicí na dalších sto let). Poté doslova hltal zbytek Legendreho a později Abela. Jeho nadšení, sebevědomí a netolerance vedly k opravdu hrozným následkům ve vztazích s učiteli a zkoušejícími. Galois se zúčastnil soutěže o vstup na Ecole Polytechnique, kolébku francouzské matematiky, ale u zkoušky neuspěl kvůli nedostatečné přípravě. Nějakou dobu poté, co se setkal s novým učitelem, který rozpoznal jeho talent, dokázal udržet svůj temperament na uzdě. V březnu 1829 Galois publikoval svůj první článek o nekonečných zlomcích, který považoval za své nejvýznamnější dílo. Poslal zprávu o svých objevech Akademii věd a Cauchy slíbil, že je představí, ale zapomněl. Navíc prostě ztratil rukopis.

Galoisův druhý neúspěch vstoupit na École Polytechnique se stal součástí matematického folklóru. Byl tak zvyklý neustále držet v hlavě složité matematické představy, že ho rozzuřilo malicherné nadržování zkoušejících. Vzhledem k tomu, že zkoušející měli potíže s pochopením jeho vysvětlení, hodil jednomu z nich do obličeje suchý mazací hadřík z tabule. Brzy nato jeho otec zemřel a spáchal sebevraždu v důsledku církevních intrik. Na jeho pohřbu prakticky vypukla vzpoura. V únoru 1830 Galois napsal následující tři články a poslal je Akademii věd na Grand Prix v matematice. Joseph Fourier, tehdejší tajemník akademie, zemřel, aniž by si je přečetl, a po jeho smrti nebyly články mezi jeho papíry nalezeny. Takový příval zklamání by přemohl každého. Galois se vzbouřil proti těm, kteří byli u moci, protože cítil, že neuznávali jeho zásluhy a zničili jeho otce. Po hlavě se vrhl do politiky a stal se zapáleným republikánem – ve Francii v roce 1830 to nebylo nejmoudřejší rozhodnutí. V posledním pokusu zaslal vědeckou práci slavnému francouzskému fyzikovi a matematikovi Simeonovi Denisovi Poissonovi (1781–1840), který reagoval tím, že požadoval další důkazy.

Tohle byla poslední kapka. V roce 1831 byl Galois dvakrát zatčen – nejprve za údajnou výzvu k zavraždění krále Ludvíka Filipa a poté, aby ho ochránily – se úřady obávaly republikánské vzpoury! Tentokrát byl odsouzen k šesti měsícům vězení na základě vykonstruovaného obvinění z nelegálního nošení uniformy rozpuštěného dělostřeleckého praporu, ke kterému vstoupil. Podmínečně propuštěn na svobodu a ujal se úkolu, který ho znechutil stejně jako všechno ostatní v životě. V dopisech svému oddanému příteli Chevalierovi je cítit jeho zklamání. 29. května 1832 přijal výzvu k souboji, jehož důvody nejsou zcela pochopeny. „Stal jsem se obětí nečestné kokety. Můj život vymírá v ubohé hádce,“ píše v „Dopisu všem republikánům“. Galoisovo nejslavnější dílo bylo načrtnuto večer před osudným soubojem. Na okrajích jsou roztroušeny stížnosti: "Už nemám čas, už nemám čas." Detailní výklad mezikroků, které nebyly pro pochopení hlavní myšlenky podstatné, byl nucen přenechat jiným. Potřeboval dát na papír základ svých objevů – původ toho, čemu se dnes říká Galoisova věta. Svou vůli zakončil tím, že požádal Chevaliera, aby „apeloval na Jacobiho a Gausse, aby vyjádřili své veřejné mínění ne o správnosti, ale o důležitosti těchto teorémů“. Brzy ráno se Galois vydal na setkání se svým rivalem. Museli střílet ze vzdálenosti 25 kroků. Galois byl zraněn a druhý den ráno zemřel v nemocnici. Bylo mu pouhých dvacet let.

Galois navázal na práci Lagrange a Cauchy, ale vyvinul obecnější metodu. To byl mimořádně důležitý úspěch v oblasti řešení kvintiky. Vědec věnoval menší pozornost původním rovnicím nebo grafické interpretaci a více se zamýšlel nad povahou samotných kořenů. Galois pro zjednodušení uvažoval pouze o tzv. ireducibilních kvintikách, tedy těch, které nebylo možné faktorizovat do tvaru polynomů nižšího řádu (jak jsme si řekli, pro jakékoli polynomické rovnice do čtvrtého řádu existují vzorce pro nalezení jejich kořeny). Obecně platí, že ireducibilní polynom s racionálními koeficienty je polynom, který nelze rozložit na jednodušší polynomy s racionálními koeficienty. Například (x 5 - 1) lze faktorizovat (x-1)(x 4 + x 3 + x 2 + x + 1), zatímco (x 5–2) Neredukovatelné. Galoisovým cílem bylo určit podmínky, za kterých lze všechna řešení obecné ireducibilní polynomiální rovnice nalézt v termínech radikálů.

Klíčem k řešení je, že kořeny jakékoli ireducibilní algebraické rovnice nejsou nezávislé, lze je vyjádřit jeden přes druhého. Tyto vztahy byly formalizovány do skupiny všech možných permutací, tzv. kořenová skupina symetrie - pro kvintiku tato skupina obsahuje 5! = 5 x 4 x 3 x 2 x 1 = 120 prvků. Matematické algoritmy Galoisovy teorie jsou velmi složité a s největší pravděpodobností, částečně v důsledku toho, byly zpočátku obtížně pochopitelné. Jakmile mu však úroveň abstrakce umožnila přejít od algebraických řešení rovnic k algebraické struktuře jejich přidružených grup, Galois byl schopen předpovědět řešitelnost rovnice na základě vlastností takových grup. Navíc jeho teorie také poskytla metodu, pomocí které lze tyto kořeny samy nalézt. Pokud jde o kvintiku, matematik Joseph Liouville (1809–1882), který v roce 1846 publikoval většinu Galoisových prací ve svém Journal of Pure and Applied Mathematics, poznamenal, že mladý vědec dokázal „krásný teorém“ a aby Je-li neredukovatelná rovnice původního stupně řešitelná pomocí radikálů, je nutné a postačující, aby všechny její kořeny byly racionálními funkcemi libovolných dvou z nich. Protože to pro kvintiku není možné, nelze to vyřešit pomocí radikálů.

Za tři roky přišel matematický svět o dvě ze svých nejjasnějších nových hvězd. Následovalo vzájemné obviňování a pátrání po duši a Abel a Galois dosáhli zaslouženého uznání, ale až posmrtně. V roce 1829 se Carl Jacobi prostřednictvím Legendra dozvěděl o Abelově „ztraceném“ rukopisu a v roce 1830 vypukl diplomatický skandál, když norský konzul v Paříži požadoval nalezení článku jeho krajana. Cauchy nakonec článek našel, ale redaktoři akademie ho znovu ztratili! Téhož roku byla Abelovi udělena Grand Prix v matematice (sdílená s Jacobim) - ale už byl mrtvý. V roce 1841 vyšla jeho biografie. V roce 1846 Liouville upravil některé Galoisovy rukopisy k publikaci a v úvodu vyjádřil politování nad tím, že akademie zpočátku odmítla Galoisovo dílo kvůli jeho složitosti – „jasnost prezentace je skutečně nezbytná, když autor vede čtenáře z vyšlapané cesty do neprobádané divočiny. území." Pokračuje: „Galois už není! Neupadejme do zbytečné kritiky. Ponechme stranou nedostatky a podívejme se na výhody! Plody Galoisova krátkého života se vešly na pouhých šedesát stran. Redaktor matematického časopisu pro kandidáty na École Normale a École Polytechnique se k případu Galois vyjádřil takto: „Kandidát s vysokou inteligencí byl vyřazen zkoušejícím s nižší úrovní myšlení. Barbarus hic ego sum, quia non intelligor illis.“

Předně druhá stránka tohoto díla není zatížena jmény, příjmeními, popisy společenského postavení, tituly a elegiemi na počest jakéhosi lakomého knížete, kterému se pomocí těchto kadidel otevře peněženka - s hrozbou zavření když chvála skončí. Neuvidíte zde pietní chvalozpěvy, psané písmeny třikrát většími než samotný text, adresované vysoce postaveným ve vědě, nějakému moudrému mecenášovi - něco povinného (řekl bych nevyhnutelného) pro někoho ve dvaceti, kdo chce něco napsat. Nikomu tady neříkám, že za všechno dobré, co z mé práce plyne, vděčím jejich radám a podpoře. Neříkám to, protože by to byla lež. Pokud bych měl zmínit některého z velikánů ve společnosti nebo ve vědě (rozdíl mezi těmito dvěma třídami lidí je v současné době téměř nepostřehnutelný), přísahám, že by to nebyl projev vděčnosti. Vděčím jim za to, že jsem první z těchto dvou článků zveřejnil tak pozdě, a že jsem to všechno napsal ve vězení – na místě, které lze jen stěží považovat za vhodné pro vědeckou reflexi, a často žasnu nad svou zdrženlivostí a schopností udržet můj hrad ve vztahu k hloupým a zlým zoilům. Myslím, že mohu použít slovo „zoiles“, aniž bych se bál, že budu obviněn z nevhodného chování, protože tak nazývám své oponenty. Nebudu zde psát o tom, jak a proč jsem byl poslán do vězení, ale musím říci, že mé rukopisy se častěji ztrácely ve spisech pánů členů akademie, i když si to popravdě nedovedu představit. indiskrétnost ze strany lidí, kteří jsou zodpovědní za Abelovu smrt. Podle mého názoru by se s tímto geniálním matematikem chtěl srovnávat každý. Postačí, když řeknu, že můj článek o teorii rovnic byl odeslán Akademii věd v únoru 1830, že výtahy z něj byly zaslány v únoru 1829, ale nic z toho nebylo vytištěno, a dokonce se ukázalo, že rukopis nelze vrátit se.

Uvažujme řešení rovnic s jednou proměnnou o stupeň vyšší než s druhou.

Stupeň rovnice P(x) = 0 je stupeň polynomu P(x), tzn. největší z mocnin jeho členů s koeficientem nerovnajícím se nule.

Takže například rovnice (x 3 – 1) 2 + x 5 = x 6 – 2 má pátý stupeň, protože po operacích otevření závorek a přivedení podobných dostaneme ekvivalentní rovnici x 5 – 2x 3 + 3 = 0 pátého stupně.

Připomeňme si pravidla, která budou potřeba k řešení rovnic stupně vyššího než dva.

Výroky o kořenech polynomu a jeho dělitelích:

1. Polynom n-tého stupně má počet kořenů nepřesahujících n a kořeny násobnosti m se vyskytují přesně mkrát.

2. Polynom lichého stupně má alespoň jeden skutečný kořen.

3. Je-li α kořenem P(x), pak P n (x) = (x – α) · Q n – 1 (x), kde Q n – 1 (x) je polynom stupně (n – 1) .

4.

5. Redukovaný polynom s celočíselnými koeficienty nemůže mít zlomkové racionální kořeny.

6. Pro polynom třetího stupně

P 3 (x) = ax 3 + bx 2 + cx + d je možná jedna ze dvou věcí: buď se rozloží na součin tří binomů

Р 3 (x) = а(х – α)(х – β)(х – γ), nebo se rozloží na součin dvojčlenu a čtvercového trinomu Р 3 (x) = а(х – α)(х 2 + βх + γ).

7. Jakýkoli polynom čtvrtého stupně může být rozšířen na součin dvou čtvercových trinomů.

8. Polynom f(x) je dělitelný polynomem g(x) beze zbytku, pokud existuje polynom q(x) takový, že f(x) = g(x) · q(x). Pro dělení polynomů se používá pravidlo „rohového dělení“.

9. Aby byl polynom P(x) dělitelný binomem (x – c), je nutné a postačující, aby číslo c bylo kořenem P(x) (důsledek Bezoutovy věty).

10. Vietův teorém: Jestliže x 1, x 2, ..., x n jsou reálné kořeny polynomu

P(x) = a 0 x n + a 1 x n - 1 + ... + a n, pak platí následující rovnosti:

x 1 + x 2 + … + x n = -a 1 /a 0,

x 1 x 2 + x 1 x 3 + ... + x n – 1 x n = a 2 /a 0,

x 1 x 2 x 3 + … + x n – 2 x n – 1 x n = -a 3 / a 0,

x 1 · x 2 · x 3 · x n = (-1) n a n/a 0 .

Řešení příkladů

Příklad 1.

Najděte zbytek dělení P(x) = x 3 + 2/3 x 2 – 1/9 krát (x – 1/3).

Řešení.

Důsledkem Bezoutova teorému: „Zbytek polynomu dělený binomem (x – c) se rovná hodnotě polynomu c. Najděte P(1/3) = 0. Zbytek je tedy 0 a číslo 1/3 je kořenem polynomu.

Odpověď: R = 0.

Příklad 2

Rozdělte „rohem“ 2x 3 + 3x 2 – 2x + 3 x (x + 2). Najděte zbytek a neúplný kvocient.

Řešení:

2x 3 + 3x 2 – 2x + 3| x + 2

2x 3 + 4 x 2 2x 2 – x

X 2 – 2 x

Odpověď: R = 3; podíl: 2x 2 – x.

Základní metody řešení rovnic vyšších stupňů

1. Zavedení nové proměnné

Způsob zavedení nové proměnné je již známý z příkladu bikvadratických rovnic. Spočívá v tom, že pro řešení rovnice f(x) = 0 se zavede nová proměnná (substituce) t = x n nebo t = g(x) a f(x) se vyjádří prostřednictvím t, čímž se získá nová rovnice r (t). Při řešení rovnice r(t) jsou nalezeny kořeny:

(ti, t2, …, t n). Poté je získána soustava n rovnic q(x) = t 1 , q(x) = t 2 , … , q(x) = t n, ze které jsou nalezeny kořeny původní rovnice.

Příklad 1.

(x 2 + x + 1) 2 – 3x 2 – 3x – 1 = 0.

Řešení:

(x 2 + x + 1) 2 – 3 (x 2 + x) – 1 = 0.

(x 2 + x + 1) 2 – 3 (x 2 + x + 1) + 3 – 1 = 0.

Substituce (x 2 + x + 1) = t.

t2 – 3t + 2 = 0.

t 1 = 2, t 2 = 1. Opačná substituce:

x 2 + x + 1 = 2 nebo x 2 + x + 1 = 1;

x 2 + x - 1 = 0 nebo x 2 + x = 0;

Odpověď: Z první rovnice: x 1, 2 = (-1 ± √5)/2, z druhé: 0 a -1.

2. Faktorizace pomocí seskupovacích a zkrácených vzorců násobení

Základ této metody také není nový a spočívá v seskupování pojmů takovým způsobem, že každá skupina obsahuje společný faktor. K tomu je někdy nutné použít nějaké umělé techniky.

Příklad 1.

x 4 – 3 x 2 + 4 x – 3 = 0.

Řešení.

Představme si - 3x 2 = -2x 2 – x 2 a skupinu:

(x 4 – 2x 2) – (x 2 – 4x + 3) = 0.

(x 4 – 2x 2 +1 – 1) – (x 2 – 4x + 3 + 1 – 1) = 0.

(x 2 – 1) 2 – 1 – (x – 2) 2 + 1 = 0.

(x 2 – 1) 2 – (x – 2) 2 = 0.

(x 2 – 1 – x + 2) (x 2 – 1 + x - 2) = 0.

(x 2 – x + 1) (x 2 + x – 3) = 0.

x 2 – x + 1 = 0 nebo x 2 + x – 3 = 0.

Odpověď: V první rovnici nejsou žádné kořeny, z druhé: x 1, 2 = (-1 ± √13)/2.

3. Faktorizace metodou neurčitých koeficientů

Podstatou metody je, že původní polynom je faktorizován neznámými koeficienty. Pomocí vlastnosti, že polynomy jsou si rovny, pokud jsou jejich koeficienty stejné při stejných mocninách, jsou nalezeny neznámé expanzní koeficienty.

Příklad 1.

x 3 + 4 x 2 + 5 x + 2 = 0.

Řešení.

Polynom stupně 3 lze rozšířit na součin lineárních a kvadratických faktorů.

x 3 + 4x 2 + 5x + 2 = (x – a)(x 2 + bx + c),

x 3 + 4x 2 + 5x + 2 = x 3 +bx 2 + cх – ax 2 – abх – ac,

x 3 + 4x 2 + 5x + 2 = x 3 + (b – a)x 2 + (cx – ab)x – ak.

Po vyřešení systému:

(b – a = 4,
(c – ab = 5,
(-ac = 2,

(a = -1,
(b = 3,
(c = 2, tj.

x 3 + 4x 2 + 5x + 2 = (x + 1) (x 2 + 3x + 2).

Kořeny rovnice (x + 1)(x 2 + 3x + 2) = 0 lze snadno najít.

Odpověď: -1; -2.

4. Metoda výběru kořene pomocí nejvyššího a volného koeficientu

Metoda je založena na aplikaci teorémů:

1) Každý celočíselný kořen polynomu s celočíselnými koeficienty je dělitelem volného členu.

2) Aby ireducibilní zlomek p/q (p je celé číslo, q přirozené číslo) byl kořenem rovnice s celočíselnými koeficienty, je nutné, aby číslo p bylo celočíselným dělitelem volného členu a 0, a q je přirozený dělitel vedoucího koeficientu.

Příklad 1.

6x 3 + 7x 2 – 9x + 2 = 0.

Řešení:

6: q = 1, 2, 3, 6.

Proto p/q = ±1, ±2, ±1/2, ±1/3, ±2/3, ±1/6.

Po nalezení jednoho kořene, například – 2, najdeme další kořeny pomocí rohového dělení, metody neurčitých koeficientů nebo Hornerova schématu.

Odpověď: -2; 1/2; 1/3.

Máte ještě otázky? Nevíte, jak řešit rovnice?
Chcete-li získat pomoc od lektora, zaregistrujte se.
První lekce je zdarma!

webové stránky, při kopírování celého materiálu nebo jeho části je vyžadován odkaz na zdroj.

Třída: 9

Základní cíle:

1. Posílit koncept celé racionální rovnice t. stupně.
2. Formulujte základní metody řešení rovnic vyšších stupňů (č > 3).
3. Naučit základní metody řešení rovnic vyšších řádů.
4. Naučte se používat typ rovnice k určení nejefektivnějšího způsobu řešení.

Formy, metody a pedagogické techniky používané učitelem ve třídě:

• Systém výuky přednáška-seminář (přednášky - výklad nové látky, semináře - řešení problémů).
• Informační a komunikační technologie (frontální průzkum, ústní práce se třídou).
• Diferencované učení, skupinové a individuální formy.
• Využití výzkumné metody ve výuce zaměřené na rozvoj matematického aparátu a myšlenkových schopností každého jednotlivého studenta.
• Tištěný materiál – individuální stručné shrnutí lekce (základní pojmy, vzorce, výroky, přednáškový materiál zhuštěný ve formě diagramů nebo tabulek).

Plán lekce:

1. Organizace času.
   Účel etapy: zapojit žáky do vzdělávací činnosti, stanovit obsah hodiny.
2. Aktualizace znalostí studentů.
   Účel etapy: aktualizovat znalosti studentů o dříve studovaných souvisejících tématech
3. Studium nového tématu (přednáška). Cíl etapy: formulovat základní metody řešení rovnic vyšších stupňů (č > 3)
4. Shrnutí.
   Účel fáze: znovu zdůraznit klíčové body v materiálu studovaném v lekci.
5. Domácí práce.
   Účel etapy: formulovat domácí úkol pro studenty.

Shrnutí lekce

1. Organizační moment.

Formulace tématu lekce: „Rovnice vyšších mocnin. Způsoby jejich řešení."

2. Aktualizace znalostí studentů.

Teoretický přehled - rozhovor. Opakování některých dříve prostudovaných informací z teorie. Studenti formulují základní definice a formulují potřebné věty. Uveďte příklady k prokázání úrovně dříve nabytých znalostí.

• Pojem rovnice s jednou proměnnou.
• Pojem kořen rovnice, řešení rovnice.
• Pojem lineární rovnice s jednou proměnnou, pojem kvadratické rovnice s jednou proměnnou.
• Pojem ekvivalence rovnic, rovnice-důsledky (koncept cizích kořenů), přechod nikoli následkem (případ ztráty kořenů).
• Koncept celého racionálního výrazu s jednou proměnnou.
• Pojem celé racionální rovnice n stupeň. Standardní tvar celé racionální rovnice. Redukovaná celá racionální rovnice.
• Přechod na sadu rovnic nižších stupňů faktorizací původní rovnice.
• Pojem polynom n stupně od X. Bezoutova věta. Důsledky Bezoutovy věty. Kořenové teorémy ( Z- kořeny a Q-odmocniny) celé racionální rovnice s celočíselnými koeficienty (redukovanými a neredukovanými).
• Hornerovo schéma.

3. Studium nového tématu.

Budeme uvažovat celou racionální rovnici n-tá mocnina standardního tvaru s jednou neznámou proměnnou x:Pn(x)= 0, kde P n (x) = a n x n + a n-1 x n-1 + a 1 x + a 0– polynom n stupně od X, A n ≠ 0. Li A n = 1 pak se taková rovnice nazývá redukovaná celočíselná racionální rovnice n stupně. Uvažujme takové rovnice pro různé hodnoty n a uveďte hlavní metody jejich řešení.

n= 1 – lineární rovnice.

n= 2 – kvadratická rovnice. Diskriminační vzorec. Vzorec pro výpočet kořenů. Vietova věta. Výběr celého čtverce.

n= 3 – kubická rovnice.

Metoda seskupování.

Příklad: x 3 – 4 x 2 – x+ 4 = 0 (x – 4) (x 2– 1) = 0 X 1 = 4 , x 2 = 1,X 3 = -1.

Reciproká kubická rovnice tvaru sekera 3 + bx 2 + bx + A= 0. Řešíme spojením členů se stejnými koeficienty.

Příklad: X 3 – 5X 2 – 5X + 1 = 0 (X + 1)(X 2 – 6X + 1) = 0 X 1 = -1, X 2 = 3 + 2, X 3 = 3 – 2.

Výběr Z-kořenů na základě věty. Hornerovo schéma. Při aplikaci této metody je nutné zdůraznit, že hledání je v tomto případě konečné a kořeny vybíráme pomocí určitého algoritmu v souladu s větou o Z-kořeny celé zadané racionální rovnice s celočíselnými koeficienty.

Příklad: X 3 – 9X 2 + 23X– 15 = 0. Rovnice je dána. Zapišme dělitele volného členu ( + 1; + 3; + 5; + 15). Aplikujme Hornerovo schéma:

Dostaneme ( X – 1)(X 2 – 8X + 15) = 0 X 1 = 1, X 2 = 3, X 3 = 5.

Rovnice s celočíselnými koeficienty. Výběr Q-kořenů na základě věty. Hornerovo schéma. Při aplikaci této metody je nutné zdůraznit, že hledání je v tomto případě konečné a kořeny vybíráme pomocí určitého algoritmu v souladu s větou o Q-kořeny neredukované celočíselné racionální rovnice s celočíselnými koeficienty.

Příklad: 9 X 3 + 27X 2 – X– 3 = 0. Rovnice je neredukovaná. Zapišme dělitele volného termínu ( + 1; + 3). Zapišme dělitele koeficientu při největší mocnině neznámé. ( + 1; + 3; + 9) Následně budeme hledat kořeny mezi hodnotami ( + 1; + ; + ; + 3). Aplikujme Hornerovo schéma:

Dostaneme ( X – )(9X 2 + 30X + 9) = 0 X 1 = , X 2 = - , X 3 = -3.

Pro usnadnění výpočtu při výběru Q -kořeny Může být vhodné provést změnu proměnné, přejít na danou rovnici a vybrat Z -kořeny.

Cardano vzorec. Pro řešení kubických rovnic existuje univerzální metoda – to je Cardanova formule. Tento vzorec je spojen se jmény italských matematiků Gerolamo Cardano (1501–1576), Nicolo Tartaglia (1500–1557) a Scipione del Ferro (1465–1526). Tento vzorec je nad rámec našeho kurzu.

n= 4 – rovnice čtvrtého stupně.

Metoda seskupování.

Příklad: X 4 + 2X 3 + 5X 2 + 4X – 12 = 0 (X 4 + 2X 3) + (5X 2 + 10X) – (6X + 12) = 0 (X + 2)(X 3 + 5X - 6) = 0 (X + 2)(X– 1)(X 2 + X + 6) = 0 X 1 = -2, X 2 = 1.

Variabilní způsob výměny.

• Bikvadratická rovnice tvaru sekera 4 + bx 2 + s = 0 .

Příklad: X 4 + 5X 2 – 36 = 0. Náhrada y = X 2. Odtud y 1 = 4, y 2 = -9. Proto X 1,2 = + 2 .

Řešíme spojením členů se stejnými koeficienty nahrazením formuláře

• Zobecněná rekurentní rovnice čtvrtého stupně tvaru sekera 4 + bx 3 + cx 2 + kbx + k 2 a = 0.

Příklad 3 . Výměna celkového pohledu(vyplývá z typu konkrétní rovnice).

n = 3.

Rovnice s celočíselnými koeficienty. Výběr Q-kořenů n = 3.

Obecný vzorec. Existuje univerzální metoda pro řešení rovnic čtvrtého stupně. Tento vzorec je spojen se jménem Ludovica Ferrariho (1522–1565). Tento vzorec je nad rámec našeho kurzu.

n > 5 – rovnice pátého a vyššího stupně.

Rovnice s celočíselnými koeficienty. Výběr Z-kořenů na základě věty. Hornerovo schéma. Algoritmus je podobný tomu, který byl popsán výše n = 3.

Rovnice s celočíselnými koeficienty. Výběr Q-kořenů na základě věty. Hornerovo schéma. Algoritmus je podobný tomu, který byl popsán výše n = 3.

Symetrické rovnice. Každá reciproká rovnice lichého stupně má kořen X= -1 a po rozdělení na faktory zjistíme, že jeden faktor má tvar ( X+ 1) a druhým faktorem je reciproká rovnice sudého stupně (její stupeň je o jeden menší než stupeň původní rovnice). Libovolná reciproká rovnice sudého stupně spolu s kořenem tvaru x = φ obsahuje také kořen druhu. Pomocí těchto tvrzení vyřešíme problém snížením stupně zkoumané rovnice.

Variabilní způsob výměny. Použití homogenity.

Obecný vzorec pro řešení celých rovnic pátého stupně neexistuje (to ukázali italský matematik Paolo Ruffini (1765–1822) a norský matematik Niels Henrik Abel (1802–1829)) a vyšších stupňů (toto ukázali např. francouzský matematik Evariste Galois (1811–1832)).

• Připomeňme ještě jednou, že v praxi je možné použít kombinace výše uvedené metody. Je vhodné přejít na sadu rovnic nižších stupňů pomocí faktoring původní rovnice.
• Mimo rámec naší dnešní diskuse jsou ty, které jsou široce používány v praxi. grafické metodyřešení rovnic a přibližné metody řešení rovnic vyšších stupňů.
• Jsou situace, kdy rovnice nemá R-kořeny.
Pak se řešení ukáže, že rovnice nemá kořeny. Abychom to dokázali, analyzujeme chování uvažovaných funkcí na intervalech monotonie. Příklad: rovnice X 8 – X 3 + 1 = 0 nemá kořeny.
• Využití vlastnosti monotonie funkcí
. Existují situace, kdy použití různých vlastností funkcí umožňuje zjednodušit úlohu.
Příklad 1: Rovnice X 5 + 3X– 4 = 0 má jeden kořen X= 1. Vzhledem k vlastnosti monotonie analyzovaných funkcí neexistují žádné další kořeny.
Příklad 2: Rovnice X 4 + (X– 1) 4 = 97 má kořeny X 1 = -2 a X 2 = 3. Po analýze chování odpovídajících funkcí na intervalech monotonie jsme dospěli k závěru, že neexistují žádné další kořeny.

4. Shrnutí.

Shrnutí: Nyní jsme zvládli základní metody řešení různých rovnic vyšších stupňů (pro n > 3). Naším úkolem je naučit se efektivně používat výše uvedené algoritmy. Podle typu rovnice se budeme muset naučit určit, která metoda řešení je v daném případě nejúčinnější, a také správně aplikovat zvolenou metodu.

5. Domácí úkol.

: odstavec 7, s. 164–174, č. 33–36, 39–44, 46.47.

: №№ 9.1–9.4, 9.6–9.8, 9.12, 9.14–9.16, 9.24–9.27.

Možná témata pro zprávy nebo abstrakty na toto téma:

• Cardano vzorec
• Grafická metoda řešení rovnic. Příklady řešení.
• Metody přibližného řešení rovnic.

Analýza studentského učení a zájmu o téma:

Zkušenosti ukazují, že zájem studentů vzbuzuje především možnost výběru Z- kořeny a Q-kořeny rovnic pomocí poměrně jednoduchého algoritmu využívajícího Hornerovo schéma. Studenty také zajímají různé standardní typy substituce proměnných, které mohou výrazně zjednodušit typ problému. Zvláště zajímavé jsou obvykle grafické metody řešení. V tomto případě můžete problémy dodatečně analyzovat pomocí grafické metody řešení rovnic; diskutujte o obecném tvaru grafu pro polynom stupně 3, 4, 5; analyzujte, jak souvisí počet kořenů rovnic stupně 3, 4, 5 se vzhledem odpovídajícího grafu. Níže je uveden seznam knih, kde naleznete další informace k tomuto tématu.

Bibliografie:

1. Vilenkin N.Ya. a další „Algebra. Učebnice pro studenty 9. ročníku s hloubkovým studiem matematiky“ - M., Prosveshchenie, 2007 - 367 s.
2. Vilenkin N.Ya., Shibasov L.P., Shibasova Z.F.„Za stránkami učebnice matematiky. Aritmetický. Algebra. 10-11 ročník“ – M., Vzdělávání, 2008 – 192 s.
3. Vygodsky M.Ya.„Příručka matematiky“ – M., AST, 2010 – 1055 s.
4. Galitsky M.L.„Sbírka úloh z algebry. Učebnice pro ročníky 8-9 s hloubkovým studiem matematiky“ - M., Prosveshchenie, 2008 - 301 s.
5. Zvavich L.I. a další „Algebra a počátky analýzy. 8–11 tříd Příručka pro školy a třídy s pokročilejším studiem matematiky“ - M., Drop, 1999 - 352 s.
6. Zvavich L.I., Averyanov D.I., Pigarev B.P., Trushanina T.N.„Úkoly z matematiky pro přípravu na písemnou zkoušku v 9. ročníku“ - M., Prosveshchenie, 2007 - 112 s.
7. Ivanov A.A., Ivanov A.P.„Tematické testy pro systematizaci znalostí z matematiky“ 1. část – M., Fizmatkniga, 2006 – 176 s.
8. Ivanov A.A., Ivanov A.P.„Tematické testy pro systematizaci znalostí v matematice“ 2. část – M., Fizmatkniga, 2006 – 176 s.
9. Ivanov A.P.„Testy a testy z matematiky. Tutorial". – M., Fizmatkniga, 2008 – 304 s.
10. Leibson K.L.„Sbírka praktických úloh z matematiky. Část 2–9 ročníků“ – M., MCNMO, 2009 – 184 s.
11. Makarychev Yu.N., Mindyuk N.G."Algebra. Doplňkové kapitoly do školní učebnice 9. ročníku. Učebnice pro studenty škol a tříd s hloubkovým studiem matematiky.“ – M., Vzdělávání, 2006 – 224 s.
12. Mordkovich A.G."Algebra. Hloubkové studium. 8. třída. Učebnice“ – M., Mnemosyne, 2006 – 296 s.
13. Savin A.P.„Encyklopedický slovník mladého matematika“ - M., Pedagogika, 1985 - 352 s.
14. Survillo G.S., Simonov A.S.„Didaktické materiály o algebře pro 9. ročník s hloubkovým studiem matematiky“ - M., Prosveshchenie, 2006 - 95 s.
15. Chulkov P.V.„Rovnice a nerovnice v kurzu školní matematiky. Přednášky 1–4“ – M., 1. září 2006 – 88 s.
16. Chulkov P.V.„Rovnice a nerovnice v kurzu školní matematiky. Přednášky 5–8“ – M., 1. září 2009 – 84 s.

Soudě podle začátku publikace, kterou zde vynecháme, text napsal Jurij Ignatievič. A je to dobře napsané a problémy jsou aktuální, ale nazvěte Rusko tak, jak to dělá Mukhin...

Bez ohledu na to, jak kdo cítí protilidovou moc, Rusko je nad ní a nezaslouží si urážky. I od talentovaného odhalovače lží americké agentury NASA.

*

Apelujte na soudruhu Mukhina Yu.I.

Všichni si vážíme vaší obětavé práce na poli odhalování lží Západu, lží Ameriky, lží pseudovědců, lží liberálů. S potěšením a přínosem pro nás i pro společnost přemýšlíme o vážných tématech, která na nás čas od času předhazujete, ať už jde o záslužnost či metafyziku, lásku k národním dějinám nebo obnovu spravedlnosti.

Vaše definice naší společné vlasti jsou však matoucí a velmi znepokojivé.

Však posuďte sami: jak byste charakterizovali člověka, který začal urážet svou matku, která byla nemocná a v důsledku toho dočasně přestala pracovat?

Ale Rusko, bez ohledu na to, jak se nazývá, a bez ohledu na to, jak dobrá nebo nechutná je vláda, Rusko je naše vlast. Vlast. Za ni naši dědové prolévali krev a položili své životy.

Proto postavit ji na roveň moci znamená snížit duchovní vznešenost na úroveň materiální, a dokonce i nízkou. Tito. porovnáváte úplně jiné kategorie. Věc nepřijatelná pro každého rozumného člověka.

Ptám se tě, drahý soudruhu. Mukhine, vážně o tom přemýšlej.

**

...A s rovnicemi (to jsem nevěděl) ​​je situace taková. Jak najít kořeny kvadratické rovnice bylo vymyšleno ve starém Egyptě.

Jak najít kořeny kubické rovnice a rovnice čtvrtého stupně bylo objeveno v šestnáctém století, ale až do roku 2016 se jim nepodařilo najít kořeny rovnice pátého stupně. A nezkoušeli to jen obyčejní lidé.

V šestnáctém století se zakladatel symbolické algebry François Viète pokusil najít kořeny rovnic pátého stupně, v devatenáctém století se zakladatel moderní vyšší algebry, francouzský matematik Evariste Galois, pokusil najít kořeny; rovnice pátého stupně se po něm pokusil najít kořeny rovnic pátého stupně norský matematik Niels Henrik Abel, který to nakonec vzdal a prokázal nemožnost řešení rovnice pátého stupně v obecné podobě.

Na Wikipedii čteme o Abelových zásluhách: „Abel dokončil brilantní studii starověkého problému:prokázal nemožnost vyřešit v obecném tvaru (v radikálech) rovnici 5. stupně...

V algebře Abel našel nezbytnou podmínku pro to, aby byl kořen rovnice vyjádřen „v radikálech“ prostřednictvím koeficientů této rovnice. Dostatečný stav brzy objevil Galois, jehož úspěchy byly založeny na práci Ábela.

Abel uvedl konkrétní příklady rovnic 5. stupně, jejichž kořeny nelze vyjádřit v radikálech, a tím do značné míry uzavřel starověký problém.

Jak vidíte, pokud se celou dobu snažili dokázat Poincarého větu a Perelman se ukázal být úspěšnější než ostatní matematici, pak po Abelovi matematici nezačali rovnice pátého stupně.

A v roce 2014 matematik z Tomsku Sergej Zaikov, o kterém lze z fotografie soudit, že je již v letech, a z údajů z článku o něm, že je absolventem Fakulty aplikované matematiky a kybernetiky Tomské státní univerzity, v průběhu své práce získané rovnice pátého stupně. Slepá ulička? Ano, je to slepá ulička! Ale Sergej Zaikov se zavázal, že to zlomí.

A v roce 2016 našel způsoby, jak řešit rovnice pátého stupně v obecné podobě! Udělal to, co se matematici Galois a Abel ukázali jako nemožné.

Snažil jsem se najít informace o Sergeji Zaikovovi na Wikipedii, ale k čertu s vámi! O matematikovi Sergeji Zaikovovi a o tom, jak našel řešení rovnic pátého stupně žádné informace!

Co dělá věc ještě pikantnější, je skutečnost, že pro matematiky existuje obdoba Nobelovy ceny - Abelova cena(Nobel zakázal dávat ceny matematikům a nyní je dávají za matematické exkrementy a nazývají je „fyzikou“).

Tato matematická cena je na počest stejného Abela, který dokázal nemožnost toho, co Zaikov udělal. Vlastní nominace na toto ocenění však není povolena. Ale Zaikov je osamělý matematik a neexistují žádné organizace, které by ho na tuto cenu mohly nominovat.

Je pravda, že máme Akademii věd, ale akademici tam nesedí, aby rozvíjeli matematiku, ale aby „vydělávali peníze“. Kdo tam potřebuje toho Zaikova?

No, pro tiskové agentury Zaikov není Perelman! Proto Zaikovův objev pro média není senzací.

Ano, Porošenko má špatné dveře! To je opravdová senzace!

Tomský matematik vyřešil problém, který nebylo možné vyřešit dvě stě let

S příchodem algebry se za její hlavní úkol považovalo řešení algebraických rovnic. Řešení rovnice druhého stupně bylo známé již v Babylonu a ve starověkém Egyptě. Ve škole procházíme podobnými rovnicemi. Pamatujete si rovnici x2 + ax + b = 0 a diskriminant?

Sergej Zaikov s knihou

Řešení algebraických rovnic třetího a čtvrtého stupně bylo nalezeno v šestnáctém století. Ale nebylo možné vyřešit rovnici pátého stupně. Lagrange našel důvod. Ukázal, že řešení rovnic třetího a čtvrtého stupně bylo možné, protože je bylo možné redukovat na rovnice, které již byly vyřešeny. Rovnici třetího stupně lze redukovat na rovnici druhého stupně a rovnici čtvrtého stupně lze redukovat na rovnici třetího. Ale rovnice pátého stupně se redukuje na rovnici šestého, tj. složitější, takže tradiční metody řešení nejsou použitelné.

Otázka řešení rovnice pátého stupně se posunula kupředu teprve před dvěma sty lety, kdy Abel dokázal, že ne všechny rovnice pátého stupně lze řešit v radikálech, tedy ve čtvercových, kubických a dalších ze školy známých kořenů. . A Galois brzy, tedy před dvěma sty lety, našel kritérium, které umožnilo určit, které rovnice pátého stupně lze řešit v radikálech a které ne. Spočívá v tom, že Galoisova skupina řešitelná v radikálech rovnice pátého stupně musí být buď cyklická, nebo metacyklická. Galois ale nenašel způsob, jak vyřešit v radikálech ty rovnice pátého stupně, které jsou řešitelné v radikálech. Galoisova teorie je velmi známá, bylo o ní napsáno mnoho knih.

Dosud byla nalezena pouze částečná řešení pro rovnice pátého stupně řešitelné radikály. A teprve letos vyřešil tomský matematik Sergej Zaikov problém, který nemohl být vyřešen po dobu dvou set let. Vydal knihu „Jak se řeší algebraické rovnice pátého stupně v radikálech“, ve které naznačil způsob řešení pro všechny rovnice pátého stupně, které jsou řešitelné v radikálech. Zaikov je absolventem Fakulty aplikované matematiky a kybernetiky Tomské státní univerzity. Podařilo se nám s ním vyzpovídat.

— Sergeji, proč jsi začal řešit tento problém?

— Potřeboval jsem řešení rovnice pátého stupně k vyřešení problému z jiného odvětví matematiky. Začal jsem zjišťovat, jak to najít, a zjistil jsem, že ne všechny jsou vyřešeny radikálně. Pak jsem se snažil najít ve vědecké literatuře způsob, jak vyřešit ty rovnice, které jsou řešitelné v radikálech, ale našel jsem pouze kritérium, podle kterého lze určit, které jsou řešitelné a které ne. Nejsem algebraista, ale samozřejmě jako absolvent FPMK umím aplikovat i algebraické metody. Proto jsem v roce 2014 vážně začal hledat řešení a sám ho našel.

Metodu jsem našel před dvěma lety, připravil jsem knihu, ve které byla nejen popsána, ale i metody řešení některých rovnic mocnin větších než pět. Ale na zveřejnění jsem neměl peníze. Letos jsem se rozhodl, že bude snazší publikovat jen část této práce, a vzal jsem z ní jen polovinu, věnovanou metodě řešení rovnice pátého stupně v radikálech.

Mým cílem je vydat něco jako návod na řešení tohoto problému, srozumitelný pro matematiky, kteří potřebují vyřešit konkrétní rovnici. Proto jsem to zjednodušil, odstranil jsem mnoho dlouhých vzorců a významnou část teorie, zkrátil jsem to o více než polovinu a nechal jsem jen to, co bylo nutné. Proto jsem vymyslel něco jako knihu „pro blbce“, ve které mohou matematici, kteří nejsou obeznámeni s Galoisovou teorií, vyřešit rovnici, kterou potřebují.

— Za to patří velký dík Vladislavu Beresněvovi, s nímž se známe již mnoho let. Sponzoroval vydání knihy.

— Je možné, abyste za vyřešení tohoto problému získali nějakou cenu v matematice? Zmínil jste například Abela. Ale existuje Abelova cena v matematice, která je považována za obdobu Nobelovy ceny?

"Tuto možnost nelze zcela vyloučit." Ale ani v to byste neměli doufat.

Například přihlášky kandidátů na Abelovu cenu za rok 2019 je třeba podat do 15. září. Navíc není povolena vlastní nominace. A jsem osamělý matematik. Neexistují žádné organizace nebo slavní matematici, kteří navrhnou mou kandidaturu. Nebude tedy uvažováno bez ohledu na to, zda si má práce tuto cenu zaslouží a zda je v duchu této ceny udělovat ji těm, kteří v Abelově díle pokračují. Ale i když se to prezentuje, vše závisí také na úrovni práce ostatních kandidátů.

Kniha je určena těm, kteří nejsou obeznámeni s Galoisovou teorií. Základy Galoisovy teorie jsou uvedeny pouze v části, ve které jsou nutné k řešení rovnice, je podrobně popsán způsob řešení a ukázány techniky, které řešení zjednodušují. Významná část knihy je věnována příkladu řešení konkrétní rovnice. Recenzenty knihy jsou doktor technických věd Gennadij Petrovič Agibalov a doktor fyziky. rohož. věd, profesor Petr Andrejevič Krylov.

PŘIPRAVENÝ ANASTASIA SKIRNEVSKAYA

Obecně platí, že rovnici stupně většího než 4 nelze vyřešit v radikálech. Ale někdy můžeme stále najít kořeny polynomu vlevo v rovnici nejvyššího stupně, pokud jej znázorníme jako součin polynomů ve stupni nejvýše 4. Řešení takových rovnic je založeno na faktorizaci polynomu, proto vám doporučujeme, abyste si toto téma prostudovali před prostudováním tohoto článku.

Nejčastěji se musíte vypořádat s rovnicemi vyšších stupňů s celočíselnými koeficienty. V těchto případech se můžeme pokusit najít racionální kořeny a potom faktorizovat polynom, abychom jej pak mohli transformovat na rovnici nižšího stupně, kterou lze snadno vyřešit. V tomto materiálu se podíváme právě na takové příklady.

Rovnice vyšších stupňů s celočíselnými koeficienty

Všechny rovnice tvaru a n x n + a n - 1 x n - 1 + . . . + a 1 x + a 0 = 0 , můžeme vytvořit rovnici stejného stupně vynásobením obou stran a n n - 1 a proměnnou změnou tvaru y = a n x:

a n x n + a n - 1 x n - 1 +. . . + a 1 x + a 0 = 0 a n n · x n + a n - 1 · a n n - 1 · x n - 1 + … + a 1 · (a n) n - 1 · x + a 0 · (a n) n - 1 = 0 y = a n x ⇒ y n + b n - 1 y n - 1 + … + b 1 y + b 0 = 0

Výsledné koeficienty budou také celočíselné. Budeme tedy muset vyřešit redukovanou rovnici n-tého stupně s celočíselnými koeficienty ve tvaru x n + a n x n - 1 + ... + a 1 x + a 0 = 0.

Vypočítáme celočíselné kořeny rovnice. Pokud má rovnice celočíselné kořeny, musíte je hledat mezi děliteli volného členu a 0 . Pojďme si je zapsat a dosadit do původní rovnosti jeden po druhém a zkontrolovat výsledek. Jakmile získáme identitu a najdeme jeden z kořenů rovnice, můžeme ji zapsat ve tvaru x - x 1 · P n - 1 (x) = 0. Zde x 1 je kořen rovnice a P n - 1 (x) je podíl x n + a n x n - 1 + ... + a 1 x + a 0 dělený x - x 1 .

Dosadíme zbývající dělitele zapsané do P n - 1 (x) = 0, počínaje x 1, protože kořeny se mohou opakovat. Po získání identity se kořen x 2 považuje za nalezený a rovnici lze zapsat ve tvaru (x - x 1) (x - x 2) · P n - 2 (x) = 0. Zde P n - 2 (x) bude podíl dělení P n - 1 (x) x - x 2.

Pokračujeme v třídění dělitelů. Najdeme všechny celé kořeny a označme jejich počet jako m. Poté může být původní rovnice reprezentována jako x - x 1 x - x 2 · … · x - x m · Pn - m (x) = 0. Zde P n - m (x) je polynom n - m stupně. Pro výpočet je vhodné použít Hornerovo schéma.

Pokud má naše původní rovnice celočíselné koeficienty, nemůžeme nakonec získat zlomkové kořeny.

Skončili jsme u rovnice P n - m (x) = 0, jejíž kořeny lze najít jakýmkoli pohodlným způsobem. Mohou být iracionální nebo komplexní.

Ukažme si na konkrétním příkladu, jak se toto schéma řešení používá.

Příklad 1

Stav: najděte řešení rovnice x 4 + x 3 + 2 x 2 - x - 3 = 0.

Řešení

Začněme hledáním celých kořenů.

Máme volný termín rovný mínus třem. Má dělitele rovné 1, - 1, 3 a - 3. Dosadíme je do původní rovnice a uvidíme, které z nich dávají výsledné identity.

Když je x rovné jedné, dostaneme 1 4 + 1 3 + 2 · 1 2 - 1 - 3 = 0, což znamená, že jedna bude kořenem této rovnice.

Nyní rozdělme polynom x 4 + x 3 + 2 x 2 - x - 3 (x - 1) ve sloupci:

Takže x 4 + x 3 + 2 x 2 - x - 3 = x - 1 x 3 + 2 x 2 + 4 x + 3.

1 3 + 2 1 2 + 4 1 + 3 = 10 ≠ 0 (- 1) 3 + 2 (- 1) 2 + 4 - 1 + 3 = 0

Máme identitu, což znamená, že jsme našli další kořen rovnice, rovný - 1.

Vydělte polynom x 3 + 2 x 2 + 4 x + 3 (x + 1) ve sloupci:

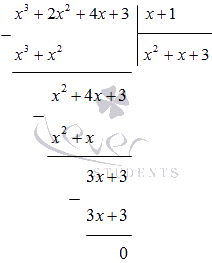
Chápeme to

x 4 + x 3 + 2 x 2 - x - 3 = (x - 1) (x 3 + 2 x 2 + 4 x + 3) = = (x - 1) (x + 1) (x 2 + x + 3)

Dosadíme dalšího dělitele do rovnosti x 2 + x + 3 = 0, počínaje - 1:

1 2 + (- 1) + 3 = 3 ≠ 0 3 2 + 3 + 3 = 15 ≠ 0 (- 3) 2 + (- 3) + 3 = 9 ≠ 0

Výsledné rovnosti budou nesprávné, což znamená, že rovnice již nemá celočíselné kořeny.

Zbývající kořeny budou kořeny výrazu x 2 + x + 3.

D = 1 2 - 4 1 3 = - 11< 0

Z toho vyplývá, že tento kvadratický trinom nemá skutečné kořeny, ale existují komplexně sdružené: x = - 1 2 ± i 11 2.

Ujasněme si, že místo dělení do sloupce lze použít Hornerovo schéma. To se provádí takto: poté, co jsme určili první kořen rovnice, vyplníme tabulku.

V tabulce koeficientů hned vidíme koeficienty podílu dělení polynomů, což znamená x 4 + x 3 + 2 x 2 - x - 3 = x - 1 x 3 + 2 x 2 + 4 x + 3 .

Po nalezení dalšího kořene, který je - 1, dostaneme následující:

Odpovědět: x = - 1, x = 1, x = - 1 2 ± i 11 2.

Příklad 2

Stav: vyřešit rovnici x 4 - x 3 - 5 x 2 + 12 = 0.

Řešení

Volný výraz má dělitele 1, - 1, 2, - 2, 3, - 3, 4, - 4, 6, - 6, 12, - 12.

Pojďme je zkontrolovat v pořadí:

1 4 - 1 3 - 5 1 2 + 12 = 7 ≠ 0 (- 1) 4 - (- 1) 3 - 5 (- 1) 2 + 12 = 9 ≠ 0 2 4 2 3 - 5 2 2 + 12 = 0

To znamená, že x = 2 bude kořenem rovnice. Vydělte x 4 - x 3 - 5 x 2 + 12 x - 2 pomocí Hornerova schématu:

Výsledkem je x - 2 (x 3 + x 2 - 3 x - 6) = 0.

2 3 + 2 2 - 3 2 - 6 = 0

To znamená, že 2 bude opět kořen. Vydělte x 3 + x 2 - 3 x - 6 = 0 x - 2:

Výsledkem je (x - 2) 2 · (x 2 + 3 x + 3) = 0.

Kontrola zbývajících dělitelů nemá smysl, protože rovnost x 2 + 3 x + 3 = 0 je rychlejší a pohodlnější řešit pomocí diskriminantu.

Pojďme vyřešit kvadratickou rovnici:

x 2 + 3 x + 3 = 0 D = 3 2 - 4 1 3 = - 3< 0

Získáme komplexně konjugovaný pár kořenů: x = - 3 2 ± i 3 2 .

Odpovědět: x = - 3 2 ± i 3 2 .

Příklad 3

Stav: Najděte skutečné kořeny rovnice x 4 + 1 2 x 3 - 5 2 x - 3 = 0.

Řešení

x 4 + 1 2 x 3 - 5 2 x - 3 = 0 2 x 4 + x 3 - 5 x - 6 = 0

Vynásobíme 2 3 na obou stranách rovnice:

2 x 4 + x 3 - 5 x - 6 = 0 2 4 x 4 + 2 3 x 3 - 20 2 x - 48 = 0

Nahradit proměnné y = 2 x:

2 4 x 4 + 2 3 x 3 - 20 2 x - 48 = 0 y 4 + y 3 - 20 y - 48 = 0

Ve výsledku jsme dostali standardní rovnici 4. stupně, kterou lze řešit podle standardního schématu. Zkontrolujme dělitele, vydělme a nakonec zjistíme, že má 2 reálné kořeny y = - 2, y = 3 a dva komplexní. Nebudeme zde uvádět celé řešení. Díky substituci budou skutečné kořeny této rovnice x = y 2 = - 2 2 = - 1 a x = y 2 = 3 2.

Odpovědět: x 1 = - 1, x 2 = 3 2

Pokud si všimnete chyby v textu, zvýrazněte ji a stiskněte Ctrl+Enter