Průmět bodu do roviny, souřadnice průmětu bodu do roviny. Promítání bodu Promítání bodu je vždy

Promítání bodu do tří rovin souřadnicových úhlových projekcí začíná získáním jeho obrazu na rovině H - horizontální promítací rovině. Za tímto účelem prochází bodem A (obr. 4.12, a) kolmým k rovině H projekční paprsek.

Na obrázku je kolmice k rovině H rovnoběžná s osou Oz. Průsečík paprsku s rovinou H (bod a) se volí libovolně. Úsek Aa určuje, v jaké vzdálenosti se nachází bod A od roviny H, čímž jasně ukazuje polohu bodu A na obrázku vzhledem k promítacím rovinám. Bod a je pravoúhlý průmět bodu A do roviny H a nazývá se vodorovný průmět bodu A (obr. 4.12, a).

Pro získání obrazu bodu A na rovině V (obr. 4.12,b) prochází projekční paprsek bodem A kolmým k čelní rovině průmětů V. Na obrázku je kolmice k rovině V rovnoběžná s osou Oy. . V rovině H bude vzdálenost od bodu A k rovině V reprezentována úsečkou aa x, rovnoběžnou s osou Oy a kolmou k ose Ox. Představíme-li si, že promítající paprsek a jeho obraz jsou vedeny současně ve směru roviny V, pak když obraz paprsku protne osu Ox v bodě a x, paprsek protne rovinu V v bodě a." Kresba z bodu a x v rovině V se získá kolmice k ose Ox, což je obraz promítajícího paprsku Aa na rovinu V, v průsečíku s promítajícím paprskem se získá bod a." Bod a" je čelní průmět bodu A, tedy jeho obraz na rovinu V.

Obraz bodu A na projekční rovině profilu (obr. 4.12, c) je sestrojen pomocí promítacího paprsku kolmého k rovině W Na obrázku je kolmice k rovině W rovnoběžná s osou Ox. Paprsek promítající z bodu A do roviny W na rovině H bude reprezentován úsečkou aa y, rovnoběžnou s osou Ox a kolmou k ose Oy. Z bodu Oy, rovnoběžného s osou Oz a kolmého k ose Oy, se sestrojí obraz promítajícího paprsku aA a v průsečíku s promítajícím paprskem se získá bod a." Bod a" je profilový průmět bodu A. , tj. obraz bodu A v rovině W.

Bod a" lze sestrojit nakreslením segmentu a"a z" z bodu a" (obraz promítajícího paprsku Aa" na rovinu V) rovnoběžného s osou Ox a z bodu az - segmentu a"a z rovnoběžného s Oy osu, dokud se neprotne s promítajícím paprskem.

Po obdržení tří průmětů bodu A na promítací roviny se úhel souřadnic rozšíří do jedné roviny, jak je znázorněno na obr. 4.11,b, spolu s průměty bodu A a promítajícími paprsky a bodem A a promítajícími paprsky Aa, Aa" a Aa" jsou odstraněny. Hrany sdružených promítacích rovin se nekreslí, ale kreslí se pouze promítací osy Oz, Oy a Ox, Oy 1 (obr. 4.13).

Analýza ortogonální kresby bodu ukazuje, že tři vzdálenosti - Aa", Aa a Aa" (obr. 4.12, c), charakterizující polohu bodu A v prostoru, lze určit vyřazením samotného promítaného objektu - bodu A, na souřadnicovém úhlu natočeném do jedné roviny (obr. 4.13). Segmenty a"a z, aa y a Oa x se rovnají Aa" jako opačné strany odpovídajících obdélníků (obr. 4.12c a 4.13). Určují vzdálenost, ve které se nachází bod A od roviny promítání profilu. Úsečky a"a x, a"a y1 a Oay jsou rovny úsečce Aa, definující vzdálenost od bodu A k vodorovné projekční rovině, úsečky aa x, a"a z a Oa y 1 jsou rovné úsečce Aa “, definující vzdálenost od bodu A k čelní rovině průmětů.

Úsečky Oa x, Oa y a Oa z, umístěné na osách promítání, jsou grafickým vyjádřením rozměrů souřadnic X, Y a Z bodu A. Souřadnice bodu jsou označeny indexem odpovídajícího písmene. . Změřením velikosti těchto segmentů můžete určit polohu bodu v prostoru, tj. nastavit souřadnice bodu.

Na diagramu jsou segmenty a"a x a aax umístěny jako jedna přímka kolmá k ose Ox a segmenty a"a z a a"a z - k ose Oz. Tyto přímky se nazývají projekční spojovací čáry. Protínají osy průmětu v bodech ax a az Spojnice průmětu spojující vodorovný průmět bodu A s profilem jedna se ukázala jako „přeříznutá“ v bodě ay.

Dva průměty stejného bodu jsou vždy umístěny na stejné spojnici průmětu, kolmé k ose průmětů.

Pro znázornění polohy bodu v prostoru stačí dva jeho průměty a daný počátek (bod O). 4.14, b dva průměty bodu zcela určují jeho polohu v prostoru Pomocí těchto dvou průmětů je možné sestrojit profilový průmět bodu A. Pokud tedy v budoucnu nebude potřeba průmět profilu, budou diagramy. být konstruován na dvou promítacích rovinách: V a H.

Rýže. 4.14. Rýže. 4.15.

Podívejme se na několik příkladů konstrukce a čtení výkresu bodu.

Příklad 1. Určení souřadnic bodu J uvedeného na diagramu ve dvou průmětech (obr. 4.14). Měří se tři segmenty: segment OB X (souřadnice X), segment b X b (souřadnice Y) a segment b X b" (souřadnice Z). Souřadnice se zapisují v tomto pořadí: X, Y a Z, za písmenem označení bodu, například B20;

Příklad 2. Sestrojení bodu na daných souřadnicích. Bod C je dán souřadnicemi C30; 10; 40. Na ose Ox (obr. 4.15) najděte bod c x, ve kterém spojnice promítání protíná osu promítání. Za tímto účelem se souřadnice X (velikost 30) vynese podél osy Ox z počátku (bod O) a získá se bod s x. Tímto bodem je nakreslena spojnice průmětu kolmo k ose Ox a z bodu je položena souřadnice Y (velikost 10), získá se bod c - horizontální průmět bodu C. Souřadnice Z (velikost 40) je položenou z bodu c x podél spojnice průmětu se získá bod c" - čelní průmět bodu C.

Příklad 3. Konstrukce profilového průmětu bodu pomocí daných průmětů. Jsou dány průměty bodu D - d a d". Bodem O se narýsují osy průmětu Oz, Oy a Оу 1 (obr. 4.16, a). Pro sestrojení průmětu profilu bodu D bod d" je průmět spojovací čára je vedena kolmo k ose Oz a pokračuje v ní doprava za osu Oz. Profilový průmět bodu D bude umístěn na této přímce Bude umístěn ve stejné vzdálenosti od osy Oz, jako je umístěn horizontální průmět bodu d: od osy Ox, tedy ve vzdálenosti dd x. Segmenty d z d" a dd x jsou stejné, protože definují stejnou vzdálenost - vzdálenost od bodu D k čelní rovině průmětů. Tato vzdálenost je souřadnicí Y bodu D.

Graficky je segment d z d" zkonstruován přenesením segmentu dd x z vodorovné roviny promítání do profilové roviny. K tomu nakreslete čáru propojení promítání rovnoběžnou s osou Ox, získáme bod d y na ose Oy ( Obr. 4.16, b Poté přeneste velikost úsečky Od y na osu Oy 1 nakreslením oblouku z bodu O o poloměru rovném úsečce Od y do průsečíku s osou Oy 1 (obr. 4.16). , b), získáme bod dy 1. Tento bod lze také sestrojit, jak je znázorněno na obr. 4.16, c, nakreslením přímky pod úhlem 45° k ose Oy z bodu d y1, promítací spojovací čára je nakreslena rovnoběžně s osou Oz a je na ni položen segment rovný segmentu d"dx, získá se bod d".

Přenesení hodnoty segmentu d x d do profilové roviny průmětů lze provést pomocí konstantní přímky výkresu (obr. 4.16, d). V tomto případě je spojovací čára promítání dd y vedena přes vodorovný průmět bodu rovnoběžného s osou Oy 1, dokud se neprotne s konstantní přímkou, a poté rovnoběžně s osou Oy, dokud se neprotne s pokračováním průmětu. spojovací vedení d"d z.

Speciální případy umístění bodů vzhledem k promítacím rovinám

Poloha bodu vzhledem k promítací rovině je určena odpovídající souřadnicí, tj. velikostí segmentu promítací spojovací čáry od osy Ox k příslušnému průmětu. Na Obr. 4.17 souřadnice Y bodu A je určena úsečkou aa x - vzdálenost bodu A k rovině V. Souřadnice Z bodu A je určena úsečkou a "a x - vzdálenost bodu A k rovině H. souřadnic je nula, pak se bod nachází na promítací rovině Obrázek 4.17 ukazuje příklady různých umístění bodů vzhledem k promítacím rovinám Souřadnice Z bodu B je rovna nule, bod se nachází v rovině H. Obr. Jeho nárysný průmět je na ose Ox a shoduje se s bodem b x Souřadnice Y bodu C je rovna nule, bod leží na rovině V, jeho horizontální průmět c je na ose Ox a shoduje se s bodem c X.

Pokud je tedy bod na promítací rovině, pak jeden z průmětů tohoto bodu leží na ose promítání.

Na Obr. 4.17 jsou souřadnice Z a Y bodu D rovny nule, proto bod D leží na ose průmětu Ox a jeho dva průměty se shodují.

Promítání bodu do roviny je speciálním případem obecného problému hledání průmětu bodu na plochu. Kvůli jednoduchosti výpočtu průmětu bodu na tečnu k ploše se při řešení obecné úlohy používá rovina jako nulová aproximace.

Zvažte problém promítání bodu do roviny definované vektorem poloměru

Budeme předpokládat, že vektory nejsou kolineární. Předpokládejme, že v obecném případě vektory nejsou ortogonální a nemají jednotkovou délku. Rovina prochází bodem, ve kterém jsou parametry rovny nule, a vektory určují parametrické směry. Daný bod má jednoznačný průmět do roviny (4.6.1). Sestrojme jednotku kolmou k rovině

Rýže. 4.6.1. Průmět bodu do roviny s(u, v)

Vypočítejme poloměrový vektor průmětu bodu do roviny jako rozdíl mezi poloměrovým vektorem průmětu bodu a složkou vektoru rovnoběžnou s normálou k rovině,

(4.6.4)

Na Obr. 4.6.1 ukazuje vektory roviny, její počáteční bod a průmět daného bodu.

Parametry a délky projekce jsou spojeny pomocí rovnic

kde kosinus úhlu mezi vektory je určen vzorcem (1.7.13).

Ze soustavy těchto rovnic zjistíme parametry průmětu bodu do roviny

(4.6.6)

kde jsou koeficienty prvního základního kvadratického tvaru roviny (1.7.8), jsou to také kovariantní složky metrického tenzoru plochy a jsou kontravariantní složky metrického tenzoru plochy. Pokud jsou vektory ortogonální, pak vzorce (4.6.6) a (4.6.7) mají tvar

Vzdálenost od bodu k jeho průmětu do roviny se obecně vypočítává jako délka vektoru. Vzdálenost od bodu k jeho průmětu do roviny lze určit bez výpočtu průmětu bodu, ale výpočtem průmětu vektoru na normálu k rovině

(4.6.8)

Speciální případy.

Průměty bodu na některé analytické plochy lze nalézt bez použití numerických metod. Chcete-li například najít průměty bodu na povrch kruhového válce, kužele, koule nebo torusu, musíte převést promítnutý bod do lokálního souřadnicového systému povrchu, kde je snadné najít parametry promítání. Podobně lze nalézt výstupky na vytlačovacích a rotačních plochách. V některých speciálních případech lze polohu promítaného bodu jeho průmětu snadno zjistit na jiných plochách.

Obecný případ.

Uvažujme problém promítání bodu na plochu v obecném případě. Předpokládejme, že potřebujeme najít všechny průměty bodu na plochu. Každý požadovaný povrchový bod splňuje systém dvou rovnic

Soustava rovnic (4.6.9) obsahuje dvě neznámé veličiny - parametry u a v. Tento problém je řešen stejně jako problém hledání průmětů daného bodu do křivky.

V první fázi určíme nulové aproximace parametrů povrchu pro průměty bodu a ve druhé fázi najdeme přesné hodnoty parametrů, které určují průměty daného bodu na plochu.

Pojďme se projít po povrchu s kroky vypočítanými pomocí vzorců (4.2.4) a (4.2.5), což je metoda pohybu přes parametrickou oblast popsaná výše. Označme parametry bodů, kterými budeme procházet . V každém bodě budeme počítat skalární součiny vektorů

(4.6.10)

Pokud požadované řešení leží blízko bodu s parametry , pak budou mít různá znaménka a budou mít také různá znaménka. Změna znamének skalárních produktů naznačuje, že požadované řešení je blízko. Berme hodnoty jako nulovou aproximaci parametrů Počínaje nulovou aproximací parametrů najdeme řešení problému s danou přesností pomocí jedné z metod řešení nelineárních rovnic. Například v Newtonově metodě při iteraci jsou přírůstky parametrů projekce zjištěny ze systému lineárních rovnic

kde jsou parciální derivace vektoru poloměru vzhledem k parametrům. Další aproximace parametrů bodové projekce se rovná . Proces zpřesňování parametrů dokončíme, až budou při další iteraci splněny nerovnosti, kde je zadaná chyba. Stejným způsobem najdeme všechny ostatní kořeny soustavy rovnic (4.6.9).

Pokud potřebujete pouze najít nejbližší průmět daného bodu na plochu, pak můžete projít stejnými body geometrického objektu a vybrat ten, který je k danému bodu nejblíže. Parametry nejbližšího bodu a by měly být zvoleny jako nulová aproximace řešení úlohy.

Promítání bodu na plochu v daném směru.

V určitých případech vzniká problém určit průmět bodu na plochu nikoli podél normály k němu, ale v daném směru. Nechť je směr promítání určen vektorem jednotkové délky q. Postavme rovnou čáru

(4.6.12)

procházející daným bodem a mající směr daného vektoru. Průměty bodu na plochu v daném směru definujeme jako průsečíky plochy s přímkou ​​(4.6.12) procházející daným bodem v daném směru.

Pr a b = |b|cos(a,b) nebo

Kde a b je skalární součin vektorů, |a| - modul vektoru a.

Instrukce. Chcete-li najít projekci vektoru Pr a b online, musíte zadat souřadnice vektorů a a b. V tomto případě lze vektor zadat v rovině (dvě souřadnice) a v prostoru (tři souřadnice). Výsledné řešení se uloží do souboru aplikace Word. Pokud jsou vektory zadány pomocí souřadnic bodů, musíte použít tuto kalkulačku.

Klasifikace vektorových projekcí

Typy projekcí podle definice vektorové projekce

1. Geometrický průmět vektoru AB na osu (vektor) se nazývá vektor A"B", jehož začátek A' je průmět začátku A na osu (vektor) a konec B' je průmět. konce B na stejnou osu.
2. Algebraické promítání vektoru AB na osu (vektor) se nazývá délka vektoru A"B", braná se znaménkem + nebo -, podle toho, zda má vektor A"B" stejný směr jako osa ( vektor).

Typy projekcí podle souřadnicového systému

Vlastnosti vektorové projekce

1. Geometrické promítání vektoru je vektor (má směr).
2. Algebraická projekce vektoru je číslo.

Věty o vektorové projekci

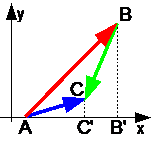AC" =AB" +B"C"

Pr a b = |b|·cos(a,b)

Typy vektorových projekcí

1. projekce na osu OX.
2. projekce na osu OY.
3. promítání do vektoru.

Projekce na ose OX	Projekce na ose OY	Projekce do vektoru
Pokud se směr vektoru A’B’ shoduje se směrem osy OX, pak promítání vektoru A’B’ má kladné znaménko.	Pokud se směr vektoru A’B’ shoduje se směrem osy OY, pak promítání vektoru A’B’ má kladné znaménko.	Pokud se směr vektoru A’B’ shoduje se směrem vektoru NM, pak promítání vektoru A’B’ má kladné znaménko.
Pokud je směr vektoru opačný než směr osy OX, pak promítání vektoru A’B’ má záporné znaménko.	Pokud je směr vektoru A’B’ opačný než směr osy OY, pak projekce vektoru A’B’ má záporné znaménko.	Pokud je směr vektoru A’B’ opačný než směr vektoru NM, pak projekce vektoru A’B’ má záporné znaménko.
Pokud je vektor AB rovnoběžný s osou OX, pak se průmět vektoru A’B’ rovná absolutní hodnotě vektoru AB.	Pokud je vektor AB rovnoběžný s osou OY, pak se průmět vektoru A’B’ rovná absolutní hodnotě vektoru AB.	Pokud je vektor AB rovnoběžný s vektorem NM, pak se projekce vektoru A’B’ rovná absolutní hodnotě vektoru AB.
Pokud je vektor AB kolmý k ose OX, pak projekce A’B’ je rovna nule (nulový vektor).	Pokud je vektor AB kolmý k ose OY, pak projekce A’B’ je rovna nule (nulový vektor).	Je-li vektor AB kolmý na vektor NM, pak projekce A’B’ je rovna nule (nulový vektor).

1. Otázka: Může mít promítání vektoru záporné znaménko? Odpověď: Ano, vektor projekce může být záporná hodnota. V tomto případě má vektor opačný směr (viz, jak je směrována osa OX a vektor AB)
2. Otázka: Může se průmět vektoru shodovat s absolutní hodnotou vektoru? Odpověď: Ano, může. V tomto případě jsou vektory rovnoběžné (nebo leží na stejné přímce).
3. Otázka: Může být projekce vektoru rovna nule (nulový vektor). Odpověď: Ano, může. V tomto případě je vektor kolmý na odpovídající osu (vektor).

Příklad 1. Vektor (obr. 1) svírá s osou OX úhel 60° (je určen vektorem a). Pokud je OE jednotka stupnice, pak |b|=4, takže .

Ve skutečnosti je délka vektoru (geometrická projekce b) rovna 2 a směr se shoduje se směrem osy OX.

Příklad 2 Vektor (obr. 2) svírá s osou OX úhel (a,b) = 120 o (s vektorem a). Délka |b| vektor b je roven 4, takže pr a b=4·cos120 o = -2.

Ve skutečnosti je délka vektoru 2 a směr je opačný než směr osy.

PROJEKTOVÁNÍ BODU NA DVĚ PROJEKČNÍ ROVINY

Vznik úsečky AA 1 lze znázornit jako výsledek pohybu bodu A v libovolné rovině H (obr. 84, a) a vznik roviny jako pohyb úsečky AB (obr. 84, b).

Bod je hlavním geometrickým prvkem přímky a plochy, proto studium pravoúhlého průmětu předmětu začíná konstrukcí pravoúhlých průmětů bodu.

Do prostoru dihedrálního úhlu tvořeného dvěma kolmými rovinami - čelní (svislou) rovinou průmětů V a horizontální rovinou průmětů H umístíme bod A (obr. 85, a).

Průsečík promítacích rovin je přímka, která se nazývá promítací osa a je označena písmenem x.

Rovina V je zde znázorněna jako obdélník a rovina H jako rovnoběžník. Nakloněná strana tohoto rovnoběžníku je obvykle nakreslena pod úhlem 45° k jeho vodorovné straně. Délka nakloněné strany se rovná 0,5 její skutečné délky.

Z bodu A se spouštějí kolmice na roviny V a H. Body a" a a průsečíku kolmiček s promítacími rovinami V a H jsou pravoúhlé průměty bodu A. Obrazec Aaa x a" v prostoru je obdélník. Boční osa tohoto obdélníku ve vizuálním obrazu je zmenšena dvakrát.

Srovnejme H roviny s V rovinou otáčením V kolem průsečíku x rovin. Výsledkem je ucelený výkres bodu A (obr. 85, b)

Pro zjednodušení složitého kreslení nejsou vyznačeny hranice promítacích rovin V a H (obr. 85, c).

Kolmice vedené z bodu A na promítací roviny se nazývají promítací přímky a základny těchto promítacích přímek - body a a a" - se nazývají průměty bodu A: a" je nárys bodu A, a je horizontální průmět. bodu A.

Čára a" a se nazývá svislá čára propojení promítání.

Umístění průmětu bodu ve složité kresbě závisí na poloze tohoto bodu v prostoru.

Leží-li bod A na vodorovné rovině průmětů H (obr. 86, a), pak se jeho vodorovný průmět a shoduje s daným bodem a průmět a" leží na ose. Když je bod B umístěn na průmětu čelní rovina průmětů V, její nárys se shoduje s tímto bodem a horizontální průmět leží na ose x Vodorovný a nárysný průmět daného bodu C, ležícího na ose x, se shoduje s tímto bodem bodů A, B a C je znázorněno na obr. 86, b. Obr.

PROJEKTOVÁNÍ BODU NA TŘI PROJEKČNÍ ROVINY

V případech, kdy si nelze představit tvar předmětu ze dvou projekcí, promítá se na tři promítací roviny. V tomto případě je zavedena promítací rovina profilu W, kolmá na roviny V a H. Vizuální znázornění soustavy tří promítacích rovin je na Obr. 87, a.

Hrany trojbokého úhlu (průsečík promítacích rovin) se nazývají promítací osy a jsou označeny x, y a z. Průsečík os promítání se nazývá začátek os promítání a označuje se písmenem O. Pusťme kolmici z bodu A na rovinu promítání W a označíme základnu kolmice písmenem „a“ získat profilový průmět bodu A.

Pro získání komplexní kresby bodu A jsou roviny H a W kombinovány s rovinou V a otáčejí se kolem os Ox a Oz. Souhrnný nákres bodu A je na Obr. 87, b a c.

Segmenty promítacích přímek z bodu A do promítacích rovin se nazývají souřadnice bodu A a jsou označeny: x A, y A a z A.

Například souřadnice z A bodu A, rovna úsečce a"a x (obr. 88, aab), je vzdálenost od bodu A k vodorovné promítací rovině H. Souřadnice y bodu A, rovna úsečka aa x, je vzdálenost bodu A k čelní rovině průmětů V. Souřadnice x A, rovna úsečce aa y - vzdálenost bodu A k rovině profilu průmětů W.

Vzdálenost mezi průmětem bodu a osou průmětu tedy určuje souřadnice bodu a je klíčem ke čtení jeho složité kresby. Ze dvou průmětů bodu lze určit všechny tři souřadnice bodu.

Pokud jsou zadány souřadnice bodu A (například x A = 20 mm, y A = 22 mm az A = 25 mm), lze sestrojit tři průměty tohoto bodu.

Za tímto účelem se od počátku souřadnic O ve směru osy Oz položí souřadnice z A a souřadnice y A se položí z konců odložených segmentů - bodů az a ay (obr 88, a) - nakreslete rovné čáry rovnoběžné s osou Ox a položte je na úsečky rovnající se souřadnici x A. Výsledné body a" a a jsou čelní a horizontální průměty bodu A.

Pomocí dvou průmětů a" a a bodu A můžete vytvořit průmět jeho profilu třemi způsoby:

1) z počátku souřadnic O nakreslete pomocný oblouk s poloměrem Oa y rovným souřadnici (obr. 87, b a c), z výsledného bodu a y1 nakreslete přímku rovnoběžnou s osou Oz a položte mimo segment rovný z A;

2) z bodu a y nakreslete pomocnou přímku pod úhlem 45° k ose Oy (obr. 88, a), získáte bod a y1 atd.;

3) z počátku souřadnic O nakreslete pomocnou přímku pod úhlem 45° k ose Oy (obr. 88, b), získáme bod a y1 atd.

Bod jako matematický pojem nemá žádné rozměry. Je zřejmé, že pokud je objekt projekce nulový rozměrový objekt, pak mluvit o jeho projekci nemá smysl.

Obr.9 Obr.10

V geometrii je vhodné považovat bod za fyzický objekt, který má lineární rozměry. Konvenčně může být za bod považována koule s nekonečně malým poloměrem. S tímto výkladem pojmu bod můžeme hovořit o jeho průmětech.

Při konstrukci ortogonálních projekcí bodu bychom se měli řídit první invariantní vlastností ortogonálního promítání: Ortogonální průmět bodu je bod.

Poloha bodu v prostoru je určena třemi souřadnicemi: X, Y, Z, zobrazující vzdálenosti, ve kterých je bod vzdálen od promítacích rovin. K určení těchto vzdáleností stačí určit body setkání těchto přímek s projekčními rovinami a změřit odpovídající veličiny, které budou indikovat hodnoty úseček podle toho X, ordináty Y a prstoklady Z bodů (obr. 10).

Průmět bodu je základna kolmice vedené z bodu do příslušné promítací roviny. Horizontální projekce body A se nazývá pravoúhlý průmět bodu na vodorovnou promítací rovinu, čelní projekce a /– respektive na čelní rovině průmětů a profil a // – na profilové rovině výstupků.

Přímo Aa, Aa / A Aa // se nazývají promítací čáry. Zároveň přímo aha, promítací bod A na vodorovnou rovinu průmětů se nazývá vodorovně promítající přímka, Aa / A Aa //- respektive: frontálně A profilové promítací linie.

Dvě promítací přímky procházející bodem A definovat rovinu, která se obvykle nazývá promítání.

Při přeměně prostorového uspořádání přední projekce bodu A – a/ zůstává na svém místě, protože patří do roviny, která nemění svou polohu během uvažované transformace. Horizontální projekce - A spolu s vodorovnou projekční rovinou se bude otáčet ve směru pohybu hodinových ručiček a bude umístěna na stejné kolmé ose X s čelní projekcí. Projekce profilu - // se bude otáčet spolu s rovinou profilu a na konci transformace zaujme polohu uvedenou na obrázku 10. V tomto případě - // bude patřit kolmici k ose Z vytažený z bodu A / a bude odstraněn z osy Z do stejné vzdálenosti jako horizontální projekce A pryč od osy X. Proto může být spojení mezi horizontálním a profilovým průmětem bodu vytvořeno pomocí dvou ortogonálních segmentů aa y A a y a // a oblouk kružnice spojující je se středem v průsečíku os ( O- původ). Označený spoj se používá k nalezení chybějícího průmětu (vzhledem ke dvěma daným). Polohu profilového (horizontálního) průmětu podle daného horizontálního (profilového) a čelního průmětu zjistíme pomocí přímky nakreslené pod úhlem 45 0 od počátku k ose. Y(tato osa se nazývá přímka k– Mongeova konstanta). První z těchto metod je výhodnější, protože je přesnější.

Proto:

1. Bod v prostoru je odstraněn:

z vodorovné roviny H Z,

z frontální roviny PROTI o hodnotu dané souřadnice Y,

z roviny profilu W podle hodnoty souřadnice. X.

2. Dva průměty libovolného bodu patří ke stejné kolmici (jedna spojnice):

horizontální a čelní – kolmé k ose X,

horizontální a profilové – kolmé k ose Y,

čelní a profilové - kolmé k ose Z.

3. Poloha bodu v prostoru je zcela určena polohou jeho dvou pravoúhlých průmětů. proto - Pomocí libovolných dvou daných ortogonálních průmětů bodu je vždy možné sestrojit jeho chybějící třetí průmět.

Pokud má bod tři konkrétní souřadnice, pak se takový bod nazývá bod obecné polohy. Pokud má bod jednu nebo dvě souřadnice, které mají nulovou hodnotu, pak se takový bod nazývá soukromý bod.

Rýže. 11 Obr. 12

Obrázek 11 ukazuje prostorový nákres bodů konkrétní polohy a obrázek 12 ukazuje komplexní nákresy (diagramy) těchto bodů. Tečka A patří do frontální roviny průmětů, bod V– vodorovná promítací rovina, bod S– rovina promítání profilu a bod D– osa x ( X).